بخش بزرگی از تکنیک های تصمیم گیری چند معیاره آنهایی هستند که داده های قطعی را می پذیرند. بدین معنا که در ماتریس تصمیم گیری صرفا می توان داده های کمی (quantitative) و یا رتبه ای (ranked) را در حالت کلامی یا عددی ولی فقط قطعی برای ارزش معیارها وارد نمود. تکنیک های تصمیم گیری چند معیاره برای داده های غیر قطعی جهت ارزش معیارها و در حالت فازی نیز توسعه داده شده است. ولی متاسفانه کمتر روشی را سراغ داریم که بتواند انواع گوناگون عدم قطعیت ها را برای ارزش معیارها پردازش نماید. NAIADE یکی از این تکنیک های ارزشمند می باشد که توسط Giuseppe Munda در سال 1995 در دانشگاه بارسلون اسپانیا توسعه داده شد. این روش قادر است با داده های غیر قطعی، نادقیق و یا ناکامل کار کند. در ذیل توضیحات این تکنیک ارائه می گردند.

1- NAIADE چیست؟

 NAIADE ( Novel Approach to Imprecise Assessment and Decision Environments) و یا “رویکردی نوین به ارزیابی غیردقیق و محیط‌های تصمیم‌گیری”، یک روش ارزیابی چندمعیاره است که مشابه دیگر تکنیک ها در این حوزه، مقایسه گزینه‌ها را بر اساس مجموعه‌ای از معیارها انجام می‌دهد. این روش امکان استفاده از اطلاعات را تحت تأثیر انواع و درجات مختلفی از عدم قطعیت فراهم می‌کند. مقادیر اختصاص داده شده به معیارها برای هر گزینه را می‌توان به صورت اعداد قطعی، تصادفی، فازی یا عبارات زبانی بیان کرد. NAIADE یک روش گسسته (مجموعه گزینه‌ها محدود و متناهی می باشند) است که از وزن‌دهی سنتی معیارها استفاده نمی‌کند. NAIADE با استفاده از نوعی از تکنیک مقایسه زوجی، گزینه‌ها را رتبه بندی می‌کند.

 
NAIADE دو نوع ارزیابی را امکان‌پذیر می‌سازد. اولین مورد بر اساس مقادیر امتیاز اختصاص داده شده به معیارهای هر گزینه است و با استفاده از ماتریس تصمیم گیری (گزینه‌ها در مقابل معیارها) انجام می‌شود. مورد دوم، تضاد بین گروه‌های ذینفع مختلف و تشکیل ائتلاف‌های احتمالی را بر اساس گزینه‌های پیشنهادی تجزیه و تحلیل می‌کند (ماتریس برابری یا Equity Matrix: ارزیابی زبانی گزینه‌ها توسط هر گروه).

2- مفاهیم در NAIADE

تحلیل چند معیاره که بر روی ماتریس تصمیم گیری انجام می‌شود، مبتنی بر یک الگوریتم مقایسه‌ای مابین گزینه‌ها است که شامل مراحل زیر می باشد:

 ۱. تکمیل ماتریس تصمیم گیری (روابطمابین معیارها/گزینه‌ها)

 ۲. مقایسه زوجی گزینه‌ها با استفاده از روابط ترجیحی

۳. تجمیع همه معیارها

۴. رتبه‌بندی گزینه‌ها

تحلیل برابری (Equity) با تکمیل ماتریس برابری انجام می‌شود که از آن یک ماتریس شباهت به دست می آید. از طریق یک الگوریتم ریاضی، می‌توان دندروگرام (dendrogram) از ائتلاف‌ها ایجاد کرد که تشکیل ائتلاف‌های احتمالی و سطح تضاد بین گروه‌های ذینفع را نشان می‌دهد.

3- ماتریس تصمیم گیری

همانند اکثر تکنیک های تصمیم گیری چندمعیاره گسسته، نقطه شروع، ایجاد ماتریس تصمیم گیری و یا معیارها/گزینه‌ها است. در ابتدا، تصمیم گیرنده باید ارزش مربوط به هر معیار را بر اساس هر گزینه تعیین کند. تصمیم گیرنده می‌تواند مقداری را به شکل یک عدد خالص و قطعی (مثلاً برای معیار هزینه، یک عدد دقیق بیان شده بر حسب واحد پول) و یا یک مقدار کمی تحت تأثیر سطوح و انواع مختلف عدم قطعیت را ارائه دهد. در مورد عدم قطعیت فازی، تصمیم گیرنده باید تابع عضویت عدد فازی را تعریف کند. در مورد عدم قطعیت تصادفی، تصمیم گیرنده باید تابع چگالی احتمال را انتخاب نماید. حتی می‌توان با استفاده از ارزیابی کیفی که توسط «متغیرهای زبانی» از پیش تعریف شده مانند «خوب»، «متوسط»، «بسیار بد» و غیره بیان می‌شود، ارزش معیاره را ارائه نمود. متغیرهای زبانی به عنوان مجموعه‌های فازی در نظر گرفته می‌شوند. NAIADE استفاده از تمامی انواع اطلاعات را مشروط بر اینکه برای هر گزینه/معیار سازگار باشند را مجاز می‌داند. البته تخصیص «انواع» مختلف (مثلاً: زبانی، فازی، تصادفی) ارزش ها به معیار یکسان برای گزینه‌های مختلف مجاز نمی باشد

4- فاصله معنایی (semantic)

برای مقایسه ارزش معیارها برای گزینه‌ها، لازم است مفهوم فاصله را بررسی نماییم. در مورد ارزیابی عددی، فاصله به سادگی به عنوان تفاوت بین دو عدد تعریف می‌شود. در ارزیابی های فازی یا تصادفی، از مفهوم فاصله معنایی استفاده می‌شود. فاصله معنایی، فاصله بین دو تابع را اندازه‌گیری می‌کند: این فاصله، موقعیت و همچنین شکل دو تابع را در نظر می‌گیرد (چه برای توابع عضویت فازی و چه برای توابع چگالی احتمال). تعریف رسمی فاصله معنایی به صورت زیر می باشد.

دو مجموعه فازی زیر را در نظر بگیرید: (رابطه 1)

[math]\mu_{{A}_{1}}{(x)}\qquad{and}\qquad\mu_{{A}_{2}}{(x)}[/math]

داریم: (رابطه 2)

[math]{f(x)=}{k_{1}}\mu_{{A}_{1}}{(x)}\qquad{and}\qquad{g((y))=}{k_{2}}\mu_{{A}_{2}}{(y)}[/math]

f(x) و g(y) توابعی هستند که از ضرب ضرایب k₁ و k₂ در توابع عضویت به دست می آیند. علت این امر نیز نرمالایز کردن توابع عضویت می باشند. (رابطه 3)

[math]\int_{-\infty}^{+\infty}{f(x)d(x)}=\int_{-\infty}^{+\infty}{g(y)d(y)}={1}[/math]

فاصله معنایی دو مجموعه فازی را می توان به صورت زیر محاسبه نمود. (رابطه 4)

[math]{S}_{d}{(f(x), g(y))}[/math]

(رابطه 5)

[math]{f(x):}\quad{X}={[x_L,}{x_U]}[/math]

(رابطه 6)

[math]{g(y):}\quad{Y}={[y_L,}{y_U]}[/math]

مجموعه های X و Y می توانند مجموعه های نامحدود هم باشند. در این حالت خواهیم داشت: (رابطه 7)

[math]{S}_{d}{(f(x), g(y))}=\int_{X}\int_{Y}\vert{x-y}\vert{f(x)g(y)dxdy}[/math]

از همین مفهوم فاصله می توان برای اندازه های تصادفی نیز استفاده نمود. در این حالت f(x) و g(y) توابع چگالی احتمال خواهند بود.

5- روابط ترجیحات و مقایسات زوجی مابین گزینه ها

مقایسه ارزش های معیارها برای هر جفت از گزینه‌ها با استفاده از فاصله معنایی که در بالا توضیح داده شد، انجام می‌شود. این مقایسه بر اساس روابط ترجیحی است که توسط تصمیم گیرنده برای هر معیار و با شروع از فاصله بین گزینه‌ها بیان می‌شود. روابط ترجیحی با استفاده از 6 تابع تعریف می‌شوند که به ازای هر معیار، شاخصی از اعتبار گزاره‌هایی مبنی بر اینکه یک گزینه بسیار بهتر، بهتر، تقریباً برابر، برابر، بدتر و بسیار بدتر از دیگری است را فراهم می‌کند. شاخص اعتبار از 0 (قطعاً نامعتبر) تا 1 (قطعاً معتبر) متغیر است و به صورت یکنواخت در این محدوده افزایش می‌یابد. در ذیل تعاریف مربوط به این شش رابطه ترجیحی آمده است:

رابطه بسیار بهتر (<<) را می توان به صورت زیر تعریف کرد: (رابطه 8)

[math]{for}\qquad{d<0}{:}[/math] [math]\qquad\qquad[/math] [math]\mu_{>>}{(d)}={0}[/math]

(رابطه 9)

[math]{for}\qquad{d>0}{:}[/math] [math]\qquad\qquad[/math] [math]\mu_{>>}{(d)}=\frac{1}{{({1+}\frac{{C^{2}_{>>}}{(\sqrt{2}-1)}}{d^2})}^{2}}[/math]

رابطه بهتر (<) می تواند به صورت زیر تعریف شود: (رابطه 10)

[math]{for}\qquad{d<0}{:}[/math] [math]\qquad\qquad[/math] [math]\mu_{>}{(d)}={0}[/math]

(رابطه 11)

[math]{for}\qquad{d>0}{:}[/math] [math]\qquad\qquad[/math] [math]\mu_{>}{(d)}=\frac{1}{{({1+}\frac{{C^{2}_{>}}}{d^2})}}[/math]

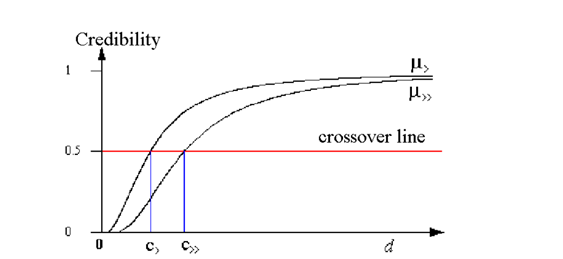
مقادیر _<C و _<<C مقادیر همگذری (crossover) هستند یعنی نقطه ای که مقدار تابع در آن برابر با 0.5 می گردد. d هم نشان دهنده فاصله می باشد. روابط ترجیحات در شکل زیر نمایش داده شده است.

شکل (1): روابط ترجیحات بهتر و بسیار بهتر

رابطه ترجیحات تقریبا مساوی به صورت ذیل تعریف می شود: (رابطه 12)

[math]\mu_\cong{(d)}={e}^{-(\frac{log(2)\vert{d}\vert}{C_\cong})}\qquad\forall{d}[/math]

رابطه ترجیحات مساوی به صورت زیر تعریف می گردد: (رابطه 13)

[math]\mu_{=}{(d)}={e}^{-(\frac{log(2){d}^{2}}{C_{==}^{2}})}\qquad\forall{d}[/math]

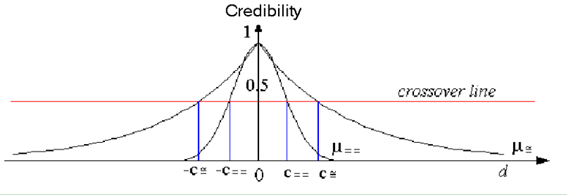
=C و ==C مقادیر همگذری (crossover) می باشند یعنی نقطه ای که مقدار تابع در آن برابر با 0.5 می گردد. d هم نشان دهنده فاصله می باشد. روابط ترجیحات در شکل زیر نمایش داده شده اند.

شکل (2): روابط ترجیحات مساوی و تقریبا مساوی

رابطه ترجیحات بسیار بدتر به صورت ذیل نوشته می شود. (رابطه 14)

[math]{for}\qquad{d>0}{:}[/math] [math]\qquad\qquad[/math] [math]\mu_{<<}{(d)}={0}[/math]

(رابطه 15)

[math]{for}\qquad{d}\leq{0}{:}[/math] [math]\qquad\qquad[/math] [math]\mu_{<<}{(d)}=\frac{1}{{({1+}\frac{{C^{2}_{<<}}{(\sqrt{2}-1)}}{d^2})}^{2}}[/math]

رابطه ترجیحات بدتر نیز به صورت ذیل خواهد بود. (رابطه 16)

[math]{for}\qquad{d>0}{:}[/math] [math]\qquad\qquad[/math] [math]\mu_{<}{(d)}={0}[/math]

(رابطه 17)

[math]{for}\qquad{d}\leq{0}{:}[/math] [math]\qquad\qquad[/math] [math]\mu_{<}{(d)}=\frac{1}{{({1+}\frac{{C^{2}_{<}}}{d^2})}}[/math]

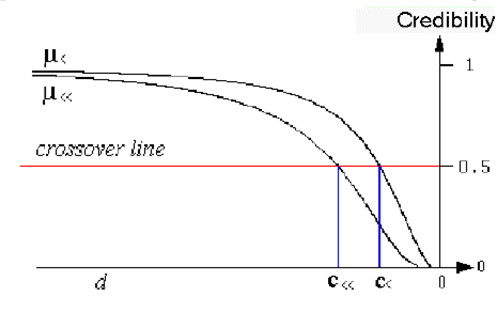
>>C و >C مقادیر همگذری (crossover) می باشند یعنی نقطه ای که مقدار تابع در آن برابر با 0.5 می گردد. d هم نشان دهنده فاصله می باشد. روابط ترجیحات در شکل زیر نمایش داده شده اند.

شکل (3): روابط ترجیحات بدتر و بسیار بدتر

محدودیت های زیر می توانند در خصوص روابط ترجیحات اعمال گردند.

محدودیت های سری اول) (رابطه 18)

[math]\mu_{>>}{(d)}=\mu_{<<}{(-d)}[/math] [math]\qquad[/math] [math]{(C_>}={-C_<)}[/math]

(رابطه 19)

[math]\mu_{>}{(d)}=\mu_{<}{(-d)}[/math] [math]\qquad[/math] [math]{(C_{>>}}={-C_{<<})}[/math]

با فرض دو گزینه A و B در فاصله d، شاخص اعتبار عبارت”A بهتر از B است” برابر با شاخص اعتبار عبارت “A بدتر از B است” خواهد بود.

محدودیت های سری دوم) (رابطه 20)

[math]{C_{==}}<{C}_\cong<{C}_{>}<{C}_{>>}[/math]

با افزایش فاصله d شاخص اعتبار عبارت” A برابر با B است” کمتر از شاخص اعتبار عبارت” A تقریباً برابر با B است” خواهد شد. با افزایش فاصله d بین A و B، شاخص اعتبار عبارت” A بسیار بهتر از B است” کمتر از شاخص اعتبار عبارت” A بهتر از B است” می گردد. علاوه بر این، مقدار همگذری ≅ C از رابطه” A تقریباً برابر با B است” باید کمتر از مقدار همگذری <C از رابطه” A بهتر از B است” باشد. به عبارت دیگر، بیان اینکه بازه ای از مقادیر فاصله وجود دارد که در آن هر دو رابطه بهتر و تقریباً برابر معتبر هستند (شاخص اعتبار بالاتر از 0.5) متناقض است.

مستقل از نوع اطلاعات (فازی، عددی یا تصادفی)، تصمیم گیرنده باید مقدار عددی فاصله را که در آن شاخص اعتبار برابر با 0.5 است (نقطه همگذری) تعیین کند. برای هر جفت از گزینه‌ها و برای هر معیار، بر اساس 6 رابطه ترجیحی تعریف شده در بخش های پیشین برای آن معیار، NAIADE تمام شاخص‌های اعتبار را محاسبه می‌کند.

6- ادغام معیارها

 NAIADE از طریق یک الگوریتم ادغام شاخص‌های اعتبار، شاخص شدت ترجیح یک گزینه را نسبت به گزینه دیگر محاسبه می‌کند. به طور خاص، پارامتر α برای بیان حداقل الزامات مورد نیاز برای شاخص‌ های اعتبار استفاده می‌شود. فقط معیارهایی که شاخص‌های آنها بالاتر از حد آستانه α باشد، در فرآیند ادغام با مقدار مثبت وارد می‌شوند. شاخص شدت μ*(a, b) از ترجیح * (که در آن * برای >>، >، ≅، =، << و < استفاده می شود) از گزینه a در مقابل b به صورت زیر تعریف می‌شود: (رابطه 21)

[math]\mu^{*}{(a,b)}=\frac{\sum_{m=1}^{M}{max(\mu{*}{(a,b)_{m}{-\alpha,{ 0})}}}}{\sum_{m=1}^{M}{max\vert\mu{*}{(a,b)_{m}{-\alpha\vert}}}}[/math]

شاخص شدت ترجیح μ*(a, b) دارای ویژگی های ذیل می باشد. (رابطه 22)

[math]{0}\leq\mu{*}{(a,b)}\leq{1}[/math]

رابطه (23)

[math]\mu{*}{(a,b)}={0}[/math] [math]\qquad\qquad[/math] [math]{if}\quad{none}\quad{of}\quad{the}\quad\mu{*}{(a,b)}_{m}\quad{is}\quad{more}\quad{than}\quad\alpha[/math]

رابطه (24)

[math]\mu{*}{(a,b)}={1}[/math] [math]\qquad\qquad[/math] [math]{if}\quad\mu{*}{(a,b)}_{m}\geq\alpha\quad\forall{m}[/math] [math]\qquad{and}[/math] [math]\quad\mu{*}{(a,b)}_{m}{>}\alpha[/math] [math]\qquad[/math] [math]{for}\quad{at}\quad{least}\quad{one}\quad{criterion.}[/math]

برای استفاده از اطلاعات مربوط به میزان تنوع در ارزیابی روابط فازی مربوط به یک معیار، از مفهوم آنتروپی استفاده می کنیم. آنتروپی شاخصی است که مابین صفر تا یک قرار دارد و نشان‌دهنده میزان تغییرات شاخص‌های اعتباری است که بالاتر از حد آستانه، و در محدوده مقدار همگذری 0.5 (حداکثر ابهام) هستند. مقدار آنتروپی صفر به این معناست که تمامی معیارها یک تجویز مشخص و دقیق (یا قطعاً معتبر یا قطعاً غیر معتبر) را ارائه می‌دهند، در حالی که مقدار آنتروپی 1 به این معنی است که تمامی معیارها نشانه ای از حداکثر ابهام را (0.5) نشان می‌دهند.

اطلاعات فراهم شده توسط شاخص شدت ترجیحات μ*(a, b) و آنتروپی وابسته به آن یعنی H*(a, b) ، می تواند درجات درستی (τ) جملات زیر را تعیین نماید:

با توجه به اکثریت معیارها:

الف – گزینه a بر گزینه b ترجیح دارد

ب – گزینه a با گزینه b بی تفاوت می باشد

ج – گزینه a از نظر ترجیح بدتر از گزینه b می باشد

سه جمله a بر b ترجیح دارد، a با b بی تفاوت می باشد و a بدتر از b است را می توان به صورت زیر محاسبه نمود: (رابطه 25)

[math]\omega_{better}{(a,b)}=\frac{\mu_{>>}{(a,b)}\circ{{C}_{>>}{(a,b)}}+\mu_{>}{(a,b)}\circ{{C}_{>}{(a,b)}}}{{C}_{>>}{(a,b)}+{C}_{>}{(a,b)}}[/math]

(رابطه 26)

[math]\omega_{indifferent}{(a,b)}=\frac{\mu_{==}{(a,b)}\circ{{C}_{==}{(a,b)}}+\mu_{\cong}{(a,b)}\circ{{C}_{\cong}{(a,b)}}}{{C}_{==}{(a,b)}+{C}_{\cong}{(a,b)}}[/math]

(رابطه 27)

[math]\omega_{worse}{(a,b)}=\frac{\mu_{<<}{(a,b)}\circ{{C}_{<<}{(a,b)}}+\mu_{<}{(a,b)}\circ{{C}_{<}{(a,b)}}}{{C}_{<<}{(a,b)}+{C}_{<}{(a,b)}}[/math]

توجه داشته باشید که: (رابطه 28)

[]{C}_{*}{(a,b)}={1-}{H}_{*}{(a,b)}[/آنتروپی وابسته به شاخص شدت ترجیح می باشد.

عملگر ○ می تواند با عملگر min به عنوان یک عملگر غیرجبرانی جایگزین شود. عملگر زیمرمن-زیسنو نیز اجازه می دهد میزان جبرانی بودن γ از صفر به معنای عدم وجود جبرانی بودن تا یک به معنای جبرانی بودن کامل تغییر نماید. (در خصوص این عملگر یک بخش جداگانه در سایت اختصاص داده خواهد شد).

در نهایت قاعده “برای بیشتر معیارها” را می توان با فیلتر نمودن ω(better), ω(indifferent), ω(worse) به صورت ذیل تفسیر نمود.

شکل (4): رابطه مربوط به اعتبار بیشتر معیارها

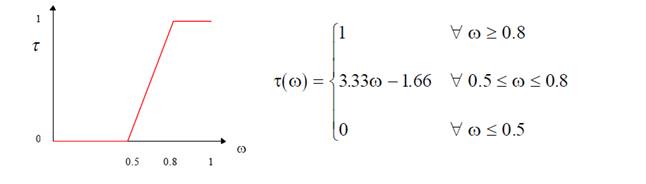
7-رتبه بندی گزینه ها

NAIADE امکان رتبه‌بندی گزینه‌ها را بر اساس شاخص‌های شدت ترجیح μ*(a,b) و آنتروپی‌های متناظر H*(a,b) فراهم می‌کند. رتبه‌بندی نهایی از اشتراک دو رتبه‌بندی جداگانه حاصل می‌شود. رتبه اول φ⁺(a) بر اساس روابط ترجیحی بهتر و خیلی بهتر ساخته می شود و با مقداری از 0 تا 1 نشان می‌دهد که a چقدر “بهتر” از همه گزینه‌های دیگر است. رتبه دوم φ^–(a) بر اساس روابط ترجیحی بدتر و خیلی بدتر بنیان نهاده می شود و مقدار آن از 0 تا 1 تغییر می‌کند که نشان می‌دهد a چقدر “بدتر” از همه گزینه‌های دیگر است. φ⁺(a) و φ^–(a) به شرح زیر محاسبه می‌شوند: (رابطه

[math]\phi^{+}{(a)}=\frac{{\sum_{n=1}^{N-1}}{(\mu_{>>}{(a,n)\circ{C}_{>>}{(a,n)}+\mu_{>}{(a,n)}\circ{C}_{>}{(a,n)})}}}{{\sum_{n=1}^{N-1}{C}_{>>}{(a,n)}+\sum_{n=1}^{N-1}{C}_{>}{(a,n)}}}[/math]

(رابطه 31)

[math]\phi^{-}{(a)}=\frac{{\sum_{n=1}^{N-1}}{(\mu_{<<}{(a,n)\circ{C}_{<<}{(a,n)}+\mu_{<}{(a,n)}\circ{C}_{<}{(a,n)})}}}{{\sum_{n=1}^{N-1}{C}_{<<}{(a,n)}+\sum_{n=1}^{N-1}{C}_{<}{(a,n)}}}[/math]

در این روابط N تعداد گزینه‌ها است و عملگر ○ دوباره می‌تواند بین عملگر حداقل که هیچ جبرانی نمی‌دهد و عملگر زیمرمن-زیسنو که درجات مختلفی از جبران γ را مجاز می‌داند (از حداقل جبران ۰ تا حداکثر جبران ۱) انتخاب شود.

8- تحلیل ذینفعان

تحلیل ذینفعان با ایجاد ماتریس ذینفعان آغاز می‌شود که نشان‌دهنده‌ی متغیرهای زبانی مربوط به قضاوت گروه‌های ذینفع برای هر یک از گزینه‌ها است. در این مورد، از فاصله‌ی معنایی (semantic) نیز برای محاسبه‌ی شاخص‌های شباهت بین گروه‌های ذینفع استفاده می‌شود. سپس یک ماتریس مشابهت بر اساس ماتریس ذینفعان محاسبه می‌شود. ماتریس مشابهت، برای هر زوج از گروه‌های ذینفع i و j، شاخصی از شباهت قضاوت در مورد گزینه‌های پیشنهادی ارائه می‌دهد. این شاخص که با s_ij نشان داده می شود به صورت s_ij=1/(1+d_ij) محاسبه می‌شود که در آن d_ij فاصله‌ی مینکوفسکی بین گروه i و گروه j است و به صورت زیر به دست می آید: (رابطه 32)

[math]{d}_{ij}=\sqrt[p]{\sum_{k=1}^{N}{(}{S}_{k}{(i,j))}^{p}}[/math]

که در آن S_k(i,j) فاصله معنایی بین گروه i و گروه j در قضاوت گزینه k و N تعداد گزینه‌هاست. p > 0 پارامتر فاصله مینکوفسکی است. از طریق دنباله‌ای از کاهش‌های ریاضی، دندروگرام تشکیل ائتلاف می تواند ساخته می‌شود. این نمودار، تشکیل ائتلاف احتمالی را برای کاهش مقادیر شاخص شباهت و درجه تضاد بین گروه‌های ذینفع نشان می‌دهد.