زندگی روزمره ما مملو از شاخص هاست: ضریب هوشی، شاخص داو جونز، GNP، کیفیت هوا، تعداد پزشکان به ازای هر هزار نفر جمعیت، شاخص فقر، شاخص موقعیت اجتماعی، شاخص قیمت مصرف کننده، نرخ بازده، … اگر روزنامه ها را بخوانید، می توانید احساس کنید که این اعداد جادویی بر جهان حکومت می کنند.  چرا این شاخص ها اینقدر قدرتمند هستند؟ احتمالاً به این دلیل که عموماً پذیرفته شده است که آنها واقعیت ها را صادقانه منعکس می کنند. این موضوع باعث می گردد تا سؤالاتی مطرح شوند.

سئوال اول) آیا یک امر واقعی در جهان وجود دارد یا چند امر واقعی وجود دارند؟ یا شاید اصلا واقعیتی وجود ندارد؟ بسیاری از فیلسوفان امروزه اعتقاد دارند که واقعیت منحصر به فرد نیست. هر فردی درک و برداشت خاصی از جهان و در نتیجه از واقعیت در این جهان دارد. می‌توان استدلال کرد که این برداشت های متفاوت از واقعیت‌، صرفا زاویه دید متفاوتی نسبت به یک واقعیت منحصر به فرد است. اما از آنجایی که نمی‌توان واقعیت را مستقل از ادراک انسان از آن واقعیت در نظر گرفت، ممکن است برخی اینگونه بیندیشند که  هیچ واقعیتی فی نفسه وجود ندارد. در نتیجه، یک شاخص ممکن است فقط برای شخصی که آن را ساخته است مناسب و مرتبط باشد.

 سئوال دوم) پاسخ سؤال قبلی هر چه که باشد، آیا می‌توانیم امیدوار باشیم که یک شاخص قادر به انعکاس واقعیت  به درستی است؟ واقعیت آنقدر پیچیده است که این موضوع می تواند مشکوک به نظر برسد.  بنابراین، باید بپذیریم که یک شاخص فقط برخی از جنبه های واقعیت را به حساب می آورد. از این رو، منطقی است بپذیریم که یک شاخص باید طوری طراحی شود که آن جنبه هایی را منعکس نماید که با دغدغه های ما مرتبط می باشند. به عنوان مثال، شاخص توسعه انسانی (HDI: Human Development Index) تعریف شده توسط برنامه توسعه سازمان ملل متحد (UNDP) برای اندازه گیری توسعه (برنامه توسعه ملل متحد 1997) را که توسط افراد مختلف در قاره های مختلف و در حوزه های مختلف فعالیت (سیاستمداران، اقتصاددانان، بازرگانان) مورد استفاده قرار می گیرد را در نظر بگیرید . آیا می توانیم فرض کنیم که دغدغه های تمام این افراد مشابه هم هستند؟

به عنوان مثال آیا نگرانی های خود سازمان ملل در ارتباط با شاخص توسعه انسانی به وضوح تعریف شده است؟ چرا آنها به این شاخص نیاز دارند؟ آیا برای قطع کمک ها به کشورهایی است که در جهت نادرست پیشرفت می کنند؟ آیا معیاری است برای تقسیم کمک ها بین فقیرترین کشورهای جهان ؟ آیا برای اعمال فشار بر دولت هایی است که بدترین عملکرد را دارند؟ آیا برای اثبات این است که  دموکراسی های غربی بهترین سیستم های سیاسی را دارند؟

 سئوال سوم) فرض کنید که هدف یک شاخص به وضوح تعریف شده باشد. آیا اطمینان داریم که این شاخص به درستی نشان می دهد که دقیقا چه چیزی را می خواهیم؟ آیا عملیات ریاضی انجام شده در حین محاسبه این شاخص واقعا با هدف این شاخص مرتبط است؟

به عنوان مثال شاخص توسعه انسانی را در نظر بگیرید که در زمره شاخص های تاثیرگذار در تصمیم گیری های جهانی و ملی می باشد.

1- شاخص توسعه انسانی

برنامه توسعه سازمان ملل متحد در سال 1997  شاخص توسعه انسانی را میانگین دستاوردهای یک کشور در سه بعد اساسی توسعه انسانی یعنی طول عمر، دانش و استاندارد زندگی معرفی می کند.

بنابراین،  HDI  یا شاخص توسعه انسانی یک شاخص ترکیبی شامل سه متغیر می باشد: امید به زندگی، پیشرفت تحصیلی (سواد بزرگسالان و ثبت نام در دوره های ابتدایی، راهنمایی و دبیرستان) و سرانه تولید ناخالص داخلی. HDI یک میانگین ساده از شاخص امید به زندگی، شاخص پیشرفت تحصیلی و شاخص سرانه تولید ناخالص داخلی می باشد. نحوه محاسبه هر یک از این شاخص ها در ذیل توضیح داده شده است:

الف- شاخص امید به زندگی

 شاخص نخست، امید به زندگی در بدو تولد را اندازه گیری می کند. به منظور نرمال سازی این شاخص، مقدار حداقل (25 سال) و حداکثر (85 سال) تعریف شده است. شاخص عبارت است از:

[math]\frac{(life-expectancy-at-birth) – 25}{85 – 25}[/math]

که مقداری بین صفر و یک دارد.

ب – شاخص پیشرفت تحصیلی (EAI: Educational Attainment Index)

این شاخص ترکیبی از دو شاخص دیگر است: شاخص سواد بزرگسالان (ALI: Adult Literacy Index) و شاخص ترکیبی نسبت ثبت نام در دبستان، راهنمایی و دبیرستان (ERI: Enrollment Ratio Index). اولی نسبت بزرگسالان باسواد به کل جمعیت بزرگسالان است در حالی که دومی نسبت کودکان در سنین دبستان، راهنمایی یا دبیرستان است که واقعاً به مدرسه می روند. EAI میانگین وزنی ALI و ERI می باشد (به ALI دو برابر وزن داده می شود).

[math]EAI=\frac{2ALI+ERI}{3}[/math]

ج- شاخص سرانه تولید ناخالص داخلی واقعی  تعدیل شده  (GDPI)   

هدف از این شاخص، اندازه گیری درآمد سرانه است. از آنجایی که ارزش یک دلار برای کسی که 100 دلار درآمد دارد بسیار بزرگتر از ارزش یک دلار برای کسی است که 100000 دلار درآمد دارد، ابتدا باید درآمد را با استفاده از فرمول اتکینسون تبدیل نمود . مقدار تبدیل شده درآمد y یعنی W(y)، به صورت زیر محاسبه  می شود:

[math]{W(y)=y}\qquad {if}\qquad {0<y<y^*},[/math]

[math]W(y)=y^* + {2[(y-y^*]^{1/2}}\qquad {if}\qquad {y^*<y<2y^*},[/math]

[math]W(y)=y^* + {2(y^*)^{1/2}} + {3[(y-2y^*)^{1/3}]}\qquad{if}\qquad {2y^*<y<3y^*},[/math]

[math]\vdots[/math]

[math]W(y)=y^* + {2(y^*)^{1/2}} + {3(y^*)^{1/3}} + \cdots +{n[(y-(n-1)y^*)^{1/n}]}[/math]

در این فرمول y درآمد است، W(y) درآمد تبدیل یافته است، و *y برابر با 5835 در نظر گرفته شده است که میانگین درآمد سالانه جهان در سال 1994 بوده است.

درآمد با فرض حداقل 100 دلار و حداکثر 40000 دلار نرمالیزه خواهد شد.

[math]\frac{({transformed}\quad {income})-W(100)}{W(40000)-W(100)}[/math]

این مقدار بین صفر و یک خواهد بود. توجه داشته باشید که W(40000)=6154 و W(100)=100 می باشد.

برخی از نکات را باید در خصوص داده ها و زمان گردآوری آنها در نظر گرفت: مقادیر شاخص توسعه انسانی به صورت سالانه محاسبه می گردند (از سال 1990). روشن است که گزارش سال 1997 حاوی اطلاعات سال 1997 نمی باشد. در اصل شاخص توسعه انسانی محاسبه شده در سال 1997، از نظر سازمان ملل متحد به عنوان شاخص توسعه در سال 1994 در نظر گرفته می شود. شاخص سال 199i (که در گزارش سال 199j آمده است) ترکیبی است از داده ها از سال 199i (برای برخی از ابعاد)با داده های سال های جدیدتر (برای دیگر ابعاد). در اینجا فقط از داده های گزارش سال 1997 استفاده خواهیم نمود که آنرا با HDR97 نشان میدهیم و کاری به اینکه در چه سالی گردآوری شده اند هم نخواهیم داشت.

برای درک چگونگی عملکرد شاخص توسعه انسانی، آنرا برای یونان محاسبه می کنیم (HDR97).

امید به زندگی در یونان 77.8 سال است. لذا داریم:

[math]LEI=\frac{(77.8-25)}{85-25}=0.880[/math]

مقدار ALI برابر با 0.967 می باشد و ERI برابر با 0.82 است. لذا خواهیم داشت:

[math]EAI=\frac{(2\times{0.967}+0.82)}{3}=0.918[/math]

مقدار واقعی GDP سرانه یونان برابر با 11265 دلار است که مقداری است مابین *y و دو برابر *y می باشد. لذا مقدار تعدیل شده GDP برای یونان عبارت است از:

[math]5835+2(11265-5835)^{1/2}=5982[/math]

[math]\frac{5982-W(100)}{W(40000)-W(100)}=\frac{5982-100}{6154-100}=0.972[/math]

در نهایت شاخص توسعه انسانی یونان برابر خواهد بود با:

[math]HDI=\frac{0.880+0.918+0.972}{3}=0.923[/math]

2- نرمالیزه کردن مقیاس

برای به دست آوردن LEI و GDPI، مقادیر حداکثر و حداقل به گونه ای تعریف شده است که پس از نرمال سازی، محدوده شاخص [0,1] باشد. انتخاب این محدوده ها کاملاً دلخواه است. مثلا چرا 25 و 85 سال؟ آیا 25 سال کمترین مقدار مشاهده شده است؟ خیر، کمترین مقدار مشاهده شده 22.6 است (گزارش شاخص توسعه انسانی برای روآندا، سال 1997). بنابراین LEI برای رواندا منفی است. مقدار 25 برای اولین گزارش (1990) انتخاب شد، زمانی که کمترین مقدار مشاهده شده بالای 35 بود. در آن زمان، هیچ کس فکر نمی کرد که امید به زندگی می تواند کمتر از 25 باشد. برای اجتناب از این وضعیت می توانستند مقدار بسیار کمتری را انتخاب کنند مثلا 20 یا 10. احتمال مشاهده مقداری کوچکتر از این حداقل، طبیعتا می باید بسیار کمتر می بود. اما از طرف دیگر انتخاب حدود پایین و بالا بدون پیآمد نیست. مثال زیر را در نظر بگیرید.

فرض کنید EAI و GDPI را برای کره جنوبی و کاستاریکا (HDR97) محاسبه کرده باشیم. امید به زندگی در بدو تولد را برای کره جنوبی و کاستاریکا می دانیم (به جدول 1 مراجعه کنید). اگر حداکثر و حداقل امید به زندگی 85 و 25 تنظیم شود، HDI برای کره جنوبی 0.890 و برای کاستاریکا 0.889 خواهد بود. اما اگر حداکثر و حداقل برای امید به زندگی 80 و 25 تنظیم شود، HDI برای کره جنوبی 0.915 و برای کاستاریکا 0.916 می گردد.

در مورد اول، کاستاریکا کمتر از کره جنوبی توسعه یافته است، در حالی که در مورد دوم کاستاریکا از کره جنوبی توسعه یافته تر می گردد. به همین دلیل است که انتخاب حدود مهم است. در واقع محدود کردن دامنه امید به زندگی از [25،85] به [25،80] اختلاف بین هر دو مقدار LEI را با یک ضریب افزایش می دهد: (85 – 25) / (80 – 25). بنابراین وزن LEI با همان ضریب افزایش خواهد یافت. در مثال ما، کاستاریکا از نظر امید به زندگی بهتر از کره جنوبی عمل کرده است. بنابراین، جای تعجب نیست که موقعیت آن با افزوده شدن بر وزن شاخص امید به زندگی در محاسبات بهبود یابد. توجه داشته باشید که ظاهراً هیچ حدودی برای ALI و ERI تعیین نشده است. در واقع، این امر معادل انتخاب 1 برای حداکثر و 0 برای حداقل مقدار می باشد. در عین حال این موضوع یک انتخاب دلخواه است. بدیهی است که مقادیر 0 و 1 تاکنون مشاهده نشده اند و قرار هم نیست در آینده نزدیک هم مشاهده گردند. بنابراین دامنه واقعی این مقیاس‌ها از [0،1] کوچکتر هستند و این امکان وجود دارد که مقیاس را با استفاده از مقادیر دیگری غیر از 0 و 1 نرمال نمود.

جدول 1. امید به زندگی در بدو تولد برای کره جنوبی و کاستاریکا

3- ویژگی جبرانی بودن

جدول 2 را در نظر بگیرید که در آن داده های دو کشور (گابن و جزایر سلیمان)، ارائه شده است. جزایر سلیمان در همه ابعاد عملکرد خوبی دارد.  ولی گابن در تمام ابعاد کمی بهتر از جزایر سلیمان است به جز امید به زندگی که در آن بسیار بدتر است. برای ما، این امید به زندگی بسیار کوتاه در گابن به وضوح نشانه توسعه نیافتگی شدید است، حتی اگر ابعاد دیگر خوب باشند.

جدول2. جبرانی بودن برای گابن و جزایر سلیمان

با این وجود،     HDI برای هر دو کشور گابن و جزایر سلیمان برابر با 0.56 است.

با توجه به این تجزیه و تحلیل و اطلاعات درون جدول 2، باید نتیجه بگیریم که گابن و جزایر سلیمان در سطح توسعه انسانی یکسان هستند. این مشکل به این دلیل به وجود آمده است که از میانگین ساده برای تجمیع داده ها در یک شاخص استفاده شده است. ویژگی میانگین ساده این است که ضعف در برخی از ابعاد می تواند با قوت در ابعاد دیگر جبران شود. این وضعیت تا حدودی مطلوب است. با این حال، ضعف های شدید را نباید جبران کرد، حتی با عملکرد بسیار خوب در ابعاد دیگر.

اجازه دهید با مفهوم جبرانی بودن بیشتر جلو برویم. از آنجایی که هر ضعفی را می توان با یک نقطه قوت جبران کرد، کاهش امید به زندگی به میزان یک سال می تواند با مقداری افزایش در تولید ناخالص داخلی واقعی تعدیل شده جبران شود (درآمد با فرمول اتکینسون تبدیل شده است). اجازه دهید این افزایش را محاسبه کنیم. هر یک سال کاهش، باعث کاهش LEI به میزان (25-85)/ 1 = 0.016667 می شود. برای جبران این کاهش، GDPI باید به همان میزان افرایش یابد. بنابراین، تولید ناخالص داخلی واقعی تعدیل شده باید با 0.016667 (100 – 6154) = 100.9 دلار افزایش یابد (به یاد بیاورید که W(40000) = 6154 می باشد).

به همین نحو، 2 سال کاهش امید به زندگی را می توان با افزایش تولید ناخالص داخلی واقعی تعدیل شده به میزان 2 برابر 100.9 دلار جبران کرد. کاهش امید به زندگی به میزان n سال را می توان با افزایش تولید ناخالص داخلی واقعی تعدیل شده به میزان n برابر 100.9 دلار جبران کرد. بنابراین ارزش یک سال زندگی 100.9 دلار است (تعدیل شده با فرمول اتکینسون). مقدار 100.9 نرخ جانشینی بین امید به زندگی و تولید ناخالص داخلی واقعی تعدیل شده نامیده می شود.

محاسبه نرخ جایگزینی دیگر آسان است: به عنوان مثال، نرخ جانشینی بین امید به زندگی و سواد بزرگسالان

 0.016667 (0 – 1) (1.5) = 0.025 است. برای جبران کاهش n سال امید به زندگی، به افزایش شاخص سواد بزرگسالان n برابر 0.025 نیاز دارید.

بگذارید اکنون از دیدگاه تولید ناخالص داخلی واقعی (تعدیل نشده) به مساله نگاه کنیم. در کشوری که تولید ناخالص داخلی واقعی آن 13071 دلار است (قبرس)، یک سال کاهش امید به زندگی را می توان با افزایش تولید ناخالص داخلی واقعی به میزان 21084 دلار جبران کرد. در کشوری که تولید ناخالص داخلی واقعی آن 700 دلار است (چاد)، یک سال کاهش امید به زندگی را می توان با افزایش 100.9 دلار در تولید ناخالص داخلی واقعی جبران نمود. از این رو همانگونه که ملاحظه می شود، امید به زندگی افراد فقیر ارزش بسیار کمتری نسبت به امید به زندگی افراد ثروتمند دارد.

4- استقلال ابعاد

مثال جدول 3 را در نظر بگیرید.

جدول 3. مثال دو کشور x وy

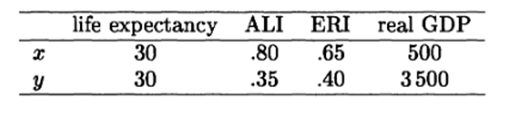
هر دو کشور x و y به یک اندازه در امید به زندگی بد هستند. y در سواد بزرگسالان از x بدتر است ولی تولید ناخالص داخلی آن بسیار بیشتر از x می باشد.

از آنجایی که امید به زندگی در هر دو کشور بسیار کوتاه است، می توان استدلال کرد که سواد بزرگسالان خیلی مهم نیست (زیرا تقریبا هیچ بزرگسالی وجود ندارد) اما درآمد مهمتر است، زیرا کیفیت زندگی را از جهات دیگر بهبود می بخشد. علاوه بر این، می توان انتظار داشت که شرایط سلامت و امید به زندگی به دلیل درآمد بالاتر به سرعت بهبود یابد. از این رو، می توان نتیجه گرفت که y  باید توسعه یافته تر از x می باشد. این نتیجه گیری توسط HDI هم تأیید می شود: 0.30 برای x و 0.34 برای y .

اجازه دهید اکنون دو کشور w و z را همانند x  و y با هم مقایسه کنیم.  امید به زندگی برای هر دو کشور w و z برابر با 70 است (جدول 4 را ببینید). در چنین شرایطی، عملکرد z در سواد بزرگسالان در مقایسه با w واقعا بد است. جمعیت بزرگسال بسیار مهم است و بی سوادی آن یک مشکل جدی محسوب می گردد. حتی اگر درآمد بالای z برای تقویت آموزش استفاده شود، دهه ها طول می کشد تا بخش قابل توجهی از جمعیت باسواد شوند. برعکس، درآمد پایین w مشکلی برای کیفیت زندگی به نظر نمی رسد، زیرا امید به زندگی و همچنین تحصیلات بالا است. از این رو، ممکن است این نتیجه گیری که w توسعه یافته تر از z است غیر منطقی نباشد. اما اگر HDI را محاسبه کنیم، 0.52 برای w و 0.56 برای z را به دست می آوریم! این موضوع عجیب نیست. هیچ تفاوتی بین x و y از یک طرف و w و z از طرف دیگر وجود ندارد، به جز امید به زندگی. اما اختلاف در امید به زندگی بین x و w و بین y و z برابر است. از این رو، این امر منجر به افزایش یکسان در  HDI در مقایسه با x و y برای هم w و هم z می شود.

جدول 4. مثال دو کشور w و z

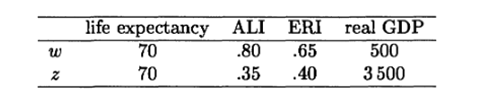
هنگامی که یک جمع (یا یک میانگین) برای ادغام ابعاد مختلف به کار برده می شود، عملکرد یکسان دو گزینه (کشور یا هر چیز دیگری) در یک یا چند بعد، در مقایسه گزینه ها با همدیگر تاثیری نخواهد داشت. ابعاد دارای مقادیر یکسان برای چند گزینه را می توان در هر جهت تغییر داد و تا زمانی که مقادیر آنها یکسان بمانند، بر نحوه مقایسه گزینه ها تأثیری نمی‌گذارند.  این ویژگی را استقلال ابعاد از همدیگر می نامند و ذاتی دو عمل جمع و میانگین می باشد.  ولی این خاصیت همیشه مطلوب نیست.  وقتی کشورها را بر اساس امید به زندگی، تحصیلات و درآمد مقایسه می‌کنیم، بعد استقلال ممکن است مطلوب نباشد.

5- ساختن مقیاس

موضوع ساختن مقیاس با نرمالیزه کردن مرتبط می باشد. اما ساختن مقیاس چیزی بیش از نرمالیزه کردن است. به عنوان مثال، در مورد تولید ناخالص داخلی واقعی، قبل از نرمال سازی، تولید ناخالص داخلی واقعی با استفاده از فرمول اتکینسون تنظیم می شود. هدف از این تعدیل واضح است: اگر 40000 دلار درآمد داشته باشید، کسب یک دلار بیشتر برایتان چندان ارزشی نخواهد داشت. ولی اگر درآمد شما  100 دلار است، کسب یک دلار بیشتر ارزشمند خواهد بود. فرمول اتکینسون همین موضوع را منعکس می کند. اما چرا باید y*=5835 انتخاب شود؟ چرا فرمول اتکینسون را انتخاب می کنیم؟ سایر فرمول ها و مقادیر دیگر برای *y نیز به همین خوبی کار می کنند. یک بار دیگر، یک انتخاب خودسرانه انجام شده است و ما به راحتی می‌توانیم یک مثال کوچک بسازیم که نشان دهد انتخاب های دلخواه دیگر (اما قابل دفاع) رتبه‌بندی های متفاوتی برای کشورها به همراه خواهد داشت.

توجه داشته باشید که این واقعیت که امید به زندگی، سواد بزرگسالان و ثبت نام ها تعدیل نشده اند نیز یک انتخاب دلخواه است. می توان استدلال کرد که بهبود امید به زندگی تا یک سال در کشوری که امید به زندگی در آن 30 سال است یک دستاورد بزرگ محسوب می گردد در حالی که در کشوری که امید به زندگی 70 سال است، همین امر موفقیت متوسطی به شمار خواهد آمد. حتی ممکن است استدلال کنند که افزایش امید به زندگی بالاتر از یک آستانه مشخص، عملا نمی تواند بهبودی به حساب آید. این امر بودجه سلامت را به اندازه ای افزایش می دهد که منابع کافی برای سایر حوزه های مهم در دسترس نمی ماند: آموزش، اشتغال و غیره.

6- جنبه های آماری

اجازه دهید چهار شاخص HDI را از نقطه نظر آماری بررسی نماییم. شاخص امید به زندگی، میانگین روی کل جمعیت می باشد و برای یک دوره زمانی مشخص از طول عمر افراد محاسبه می شود. میانگین ها، حتی اگر مفید هم باشند، نمی توانند پراکندگی موجود در جمعیت را منعکس کنند. در کشوری که تقریباً همه تا 50 سالگی در آن عمر می کنند، امید به زندگی هم 50 سال است،در حالیکه  کشوری که در آن بخشی از جمعیت (به هر دلیلی) عمر کمتر از 50 سال دارند و بخشی دیگر از جمعیت تا 80 سالگی زندگی می کنند نیز ممکن است امید به زندگی 50 سال باشد. توجه داشته باشید که این نوع از میانگین کاملاً خاص است.  فرض کنید چند تخمین از وزن نامعلوم یک جسم را در دست داریم، در این حالت  میانگین این تخمین ها میتواند برآورد خوبی از وزن واقعی آن جسم در نظر گرفته شود. وزن یک جسم واقعاً وجود دارد در حالیکه طول عمر یک موجودیت فیزیکی نیست. طول عمر متوسط در حقیقت طول عمر یک انسان ایده آل یا متوسط می باشد که عملا وجود خارجی ندارد و صرفا سمبولیک تلقی می شود. دیگر انسان ها همچون نسخه هایی ناقص از این انسان متوسط هستند.

  تا قرن نوزدهم، این دو نوع میانگین‌ با نام‌های متفاوتی نامیده می‌شدند و دو مقوله کاملاً متفاوت در نظر گرفته می‌شدند. در طول قرن نوزدهم، ستاره شناس بلژیکی کوتلت (1894-1796) مفهوم انسان متوسط ​​را ابداع کرد و هر دو نوع میانگین را تبدیل به تنها یک میانگین نمود.  

برای متقاعد کردن شما به اینکه مفهوم انسان متوسط مفهومی بسیار عجیب است (علیرغم احتمالاً مفید بودن)، کشوری را در نظر بگیرید که در تمامی ساکنان آن مثلث های قائم الزاویه با اندازه ها و اشکال مختلف هستند. برای سهولت،  فرض کنیم که فقط دو نوع مثلث قائم الزاویه با نسبت های یکسان وجود دارد (شکل 1).یک آماردان تصمیم می گیرد مثلث قائم الزاویه متوسط را به دست آورد. به همین منظور میانگین اضلاع متناظر مثلث ها را محاسبه می کند و آنچه که به دست می آورد مثلثی است با یال هایی به طول 4، 8 و 9. یعنی مثلثی که اصلا قائم الزاویه نیست.

[math]4^2+8^2\neq9^2[/math]

میانگین مثلث های قائم الزاویه یک مثلث قائم الزاویه نیست!  زاویه قائمه در چنین مثلثی در واقع یک زاویه تقریباً 91 درجه خواهد بود. به همین ترتیب،  کوتلت اندازه متوسط ​​انسان ها را در همه ابعاد، از جمله کبد، قلب، طحال و سایر اندام ها اندازه گیری کرد. چیزی که او به دست آورد یک انسان میانگین بود که امکان در کنار هم گذاردن تمامی اندام های متوسط در بدن وی غیرممکن بود. آنها خیلی بزرگ بودند!

شاخص سواد بزرگسالان مقوله ای کاملاً متفاوت است: این شاخص تعداد بزرگسالان باسواد است که بر کل جمعیت بزرگسالان تقسیم شده است تا امکان مقایسه بین کشورها فراهم شود. بنابراین می توان فکر کرد که میانگین نیست. این امر در واقع بستگی به چگونگی تفسیر ما از موضوع دارد. اگر در نظر بگیریم که ALI   برابر با 0.6 به این معنی است که 60 درصد جمعیت باسواد هستند، پس میانگین نیست. ولی اگر در نظر بگیریم که ALI برابر با 0.6  به این معنی است که میانگین سطح سواد در یک کشور  60٪ است، آنگاه یک میانگین خواهد بود. البته این تفسیر آخر احمقانه تر از محاسبه شاخص امید به زندگی نیست.

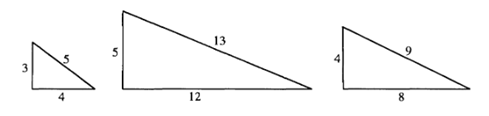
شکل 1. دو مثلث قائم الزاویه و میانگین آنها

متغیری را در نظر بگیرید که مقدار آن برای یک بزرگسال بی سواد 0 و برای یک فرد باسواد 1 باشد.  میانگین این متغیر را در کل جمعیت و در یک دوره زمانی محاسبه کنید. چه چیزی بدست می آورید؟ شاخص سواد بزرگسالان!

ما می توانیم شاخص نسبت ثبت نام و شاخص تولید ناخالص داخلی واقعی تعدیل شده را هم به همان شیوه ALI تجزیه و تحلیل کنیم. آنها مقادیری هستند که در سطح کشور اندازه گیری می شوند. اولی یک نسبت است و دومی مقداری نرمالیزه شده است ومی توان آنها را در سطح فردی همانند میانگین ها تفسیر کرد. در مورد خود HDI چه قضاوتی می توان داشت؟

 بر اساس برنامه توسعه سازمان ملل متحد در سال  (1997)، HDI طراحی شده است تا بتواند میانگین دستاوردهای یک کشور را اندازه گیری کند.

…اندازه گیری میانگین دستاوردها در یک کشور…

علاوه بر این، HDI حاوی یک شاخص (LEI) است که تنها با در نظر گرفتن مفهوم انسان متوسط  کوتلت  قابل تفسیر می باشد. بنابراین ALI، GDPI و HDI نیز باید از این دیدگاه تفسیر شوند.

در حقیقت HDI به نوعی توصیف می کند که انسان متوسط ​​در یک کشور خاص چقدر توسعه یافته است.

Evaluation and Decision Models: A Critical Perspective

Bouyssou, Marchant, Pirlot, Perny, Tsoukias, Vincke

Kluwer Academic Publishers (2000)