یکی از موضوعات جالب در بحث اعداد فازی، عملیات جبری روی این اعداد می باشد. اصولا به دلیل اینکه هر عدد فازی ، یک مجموعه فازی محسوب می گردد، انجام عملیات جبری روی مجموعه ها دارای مفهومی متفاوت از انجام این عملیات روی اعداد عادی است. در میان این عملیات، حاصلضرب از جایگاه ویژه ای برخوردار می باشد و معمولا از نظر دانشجویان موضوعی بحث برانگیز تلقی می گردد. به دلیل تنوع مجموعه های فازی و لاجرم اعداد فازی، که طبعا حالت خاصی از مجموعه های فازی می باشند، مفهوم ضرب می تواند متفاوت باشد. لذا در این مقاله به ضرب پرکاربردترین اعداد فازی یعنی اعداد مثلثی خواهم پرداخت (دلیل پر کاربرد بودن اعداد فازی مثلثی را در مقاله ای در همین سایت می توانید مشاهده نمایید).

روشی را که در این مقاله به آن خواهم پرداخت، بر اساس ضرب اعداد بازه ای قرار دارد. لذا اجازه دهید تا در ابتدا در خصوص ضرب دو عدد بازه ای بحثی داشته باشیم.

دو عدد بازه ای A و B به صورت ذیل تعریف شده اند:

[math]{A=[}{a}_{1}{,}{a}_{2}{]}\qquad{B=[}{b}_{1}{,}{b}_{2}{]}\qquad\qquad{(1)}[/math]

حاصلضرب این دو عدد بازه ای عبارت است از:

[math]{A.B}={[}{a}_{1}{.}{b}_{1}\bigwedge{a}_{1}{.}{b}_{2}\bigwedge{a}_{2}{.}{b}_{1}\bigwedge{a}_{2}{.}{b}_{2}\quad{,}\quad{a}_{1}{.}{b}_{1}\bigvee{a}_{1}{.}{b}_{2}\bigvee{a}_{2}{.}{b}_{1}\bigvee{a}_{2}{.}{b}_{2}{]}\qquad\qquad{(2)}[/math]

علایم به کار رفته در رابطه فوق به عنوان “و” و “یا” منطقی هم تلقی میگردند ولی در اینجا مقصود از آنها min و max می باشد.

[math]\bigwedge\qquad{(min)}[/math]

[math]\bigvee\qquad{(max)}[/math]

برای درک بهتر ارتباط مابین یک عدد فازی مثلثی و یک عدد بازه ای، شکل زیر را در نظر بگیرید. این شکل نشان دهنده عدد فازی مثلثی (20,60,100) می باشد. اگر برش آلفا روی این عدد فازی زده شود، بازه پشتیبان به دست آمده یک عدد بازه ای به صورت [40,80] خواهد شد.

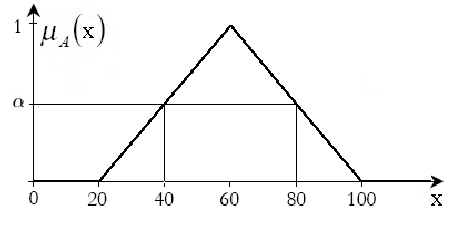
حال اجازه دهید به سراغ ضرب اعداد فازی مثلثی در یکدیگر برویم.

دو عدد فازی مثلثی زیر را در نظر بگیرید:

[math]\widetilde{M}={(a}_{1}{,}{b}_{1}{,}{c}_{1}{)}\qquad\qquad{(3)}[/math]

[math]\widetilde{N}={(a}_{2}{,}{b}_{2}{,}{c}_{2}{)}\qquad\qquad{(4)}[/math]

اگر برش آلفا را برای هر کدام از این اعداد مثلثی در نظر بگیریم، بازه پشتیبان برش به صورت اعداد بازه ای زیر قابل تعریف خواهند بود.

[math]{M}_\alpha={[}{m_\alpha}^{L}{,}\quad{m_\alpha}^{R}{]}={[}{(}{b}_{1}{-}{a}_{1}{)}{.}\alpha{+}{a}_{1}{,}{(}{b}_{1}{-}{c}_{1}{)}{.}\alpha+{c}_{1}{]}\qquad\qquad{(5)}[/math]

[math]{N}_\alpha={[}{n_\alpha}^{L}{,}\quad{n_\alpha}^{R}{]}={[}{(}{b}_{2}{-}{a}_{2}{)}{.}\alpha{+}{a}_{2}{,}{(}{b}_{2}{-}{c}_{2}{)}{.}\alpha+{c}_{2}{]}\qquad\qquad{(6)}[/math]

[math]\widetilde{Q}=\widetilde{M}\otimes\widetilde{N}\Longrightarrow{[}{m_\alpha}^{L}{,}\quad{m_\alpha}^{R}{]}\times{[}{n_\alpha}^{L}{,}\quad{n_\alpha}^{R}{]}={[}{q_\alpha}^{L}{,}\quad{q_\alpha}^{R}{]}\qquad\qquad{(7)}[/math]

[math]{q}_\alpha^{L}={min}\lbrace{m}_\alpha^{L}{.}{n}_\alpha^{L}\quad{,}\quad{m}_\alpha^{L}{.}{n}_\alpha^{R}\quad{,}\quad{m}_\alpha^{R}{.}{n}_\alpha^{L}\quad{,}\quad{m}_\alpha^{R}{.}{n}_\alpha^{R}\rbrace\qquad\qquad{(8)}[/math]

[math]{q}_\alpha^{R}={max}\lbrace{m}_\alpha^{L}{.}{n}_\alpha^{L}\quad{,}\quad{m}_\alpha^{L}{.}{n}_\alpha^{R}\quad{,}\quad{m}_\alpha^{R}{.}{n}_\alpha^{L}\quad{,}\quad{m}_\alpha^{R}{.}{n}_\alpha^{R}\rbrace\qquad\qquad{(9)}[/math]

روابط (8) و (9) به صورت زیر تبدیل خواهند شد:

[math]{q}_\alpha^{L}={m}_\alpha^{L}{.}{n}_\alpha^{L}\qquad\qquad{(10)}[/math]

[math]{q}_\alpha^{R}={m}_\alpha^{R}{.}{n}_\alpha^{R}\qquad\qquad{(11)}[/math]

با فرض اینکه داشته باشیم:

[math]{a}_{1}\leq{b}_{1}\leq{c}_{1}\qquad{and}\qquad{a}_{2}\leq{b}_{2}\leq{c}_{2}[/math]

در نتیجه خواهیم داشت:

[math]{q}_\alpha^{L}={(}{b}_{1}{-}{a}_{1}{)}{.}{(}{b}_{2}{-}{a}_{2}{)}{.}\alpha^{2}{+}{(}{a}_{1}{b}_{2}+{a}_{2}{b}_{1}-{2}{a}_{1}{a}_{2}{)}\alpha{+}{a}_{1}{a}_{2}\qquad\qquad{(12)}[/math]

[math]{q}_\alpha^{R}={(}{b}_{1}{-}{c}_{1}{)}{.}{(}{b}_{2}{-}{c}_{2}{)}{.}\alpha^{2}{+}{(}{c}_{1}{b}_{2}+{c}_{2}{b}_{1}-{2}{c}_{1}{c}_{2}{)}\alpha{+}{c}_{1}{c}_{2}\qquad\qquad{(13)}[/math]

به عنوان مثال دو عدد فازی مثلثی زیر را در نظر بگیرید:

[math]\widetilde{M}={(20,60,100)}\qquad\qquad\widetilde{N}={(10,70,90)}[/math]

با فرض برش آلفا برابر با 0.6، حاصلضرب این دو عدد فازی عدد بازه ای ذیل را به دست خواهد داد.

[math]\widetilde{Q}=\widetilde{M}\otimes\widetilde{N}[/math]

[math]{q}_\alpha^{L}={(60-20)(70-10)}\times{(0.6)}^{2}+{(20}\times{70}+{10}\times{60}{-}{2}\times{20}\times{10)}\times{0.6}+{20}\times{10}[/math]

[math]{q}_\alpha^{R}={(60-100)(70-90)}\times{(0.6)}^{2}+{(100}\times{70}+{90}\times{60}{-}{2}\times{100}\times{90)}\times{0.6}+{100}\times{90}[/math]

[math]\widetilde{Q}={[1064,9288]}[/math]