معمولا در پاسخ به سئوال فوق، ساده بودن استفاده از اعداد فازی مثلثی علت اصلی شمرده می شود. بعضی ها هم می گویند چون دیگران بیشترین استفاده را از این نوع اعداد فازی کرده اند پس ما هم همان کار را می کنیم.

ولی آیا این پاسخ ها می توانند قانع کننده باشند؟ مطمئنا خیر. برای یافتن پاسخ درست اجازه دهید تا در ابتدا برخی مفاهیم را با هم مرور کنیم. نخستین مورد، تفاوت بین احتمالات عینی و ذهنی است.

(Objective and Subjective Probabilities)

1- احتمالات عینی و ذهنی

برای تعریف احتمالات عینی، در اینجا به شکلی ساده تئوری بسامدی کارل پوپر را توضیح خواهم داد. این تئوری در خصوص احتمالات، نزدیکی بسیار زیادی با تئوری مجموعه ها دارد.

هر پدیده تصادفی مجموعه ای از پیامدها را به عنوان ویژگی اصلی خود به همراه دارد که به آن فضای نمونه گفته می شود. به بیان دیگر، امکان ندارد که نتایج پدیده تصادفی خارج از این فضای نمونه باشند. مثلا فضای نمونه حاصل از انداختن یک تاس، شش عدد ثبت شده روی وجوه تاس است که در نتیجه پرتاب تاس قابل مشاهده خواهند بود.

ممکن است اعضای فضای نمونه عددی باشند، ممکن هم هست که غیر عددی باشند. مثلا فضای نمونه حاصل از انداختن یک تاس غیر عددی است (وجوه تاس). می توانیم با اختصاص یک عدد به هر عضو فضای نمونه، آنها را از شکل غیر عددی به عددی تبدیل نماییم (طبیعی است که اگر اعضای فضای نمونه از ابتدا عددی باشند دیگر نیازی به این کار نخواهد بود). این اعداد را متغیر تصادفی می نامیم که در مورد تاس گسسته هستند، ولی می توانند در موارد دیگر پیوسته هم باشند.

علیرغم تفاوت مابین مفهوم فضای نمونه  و مفهوم متغیر تصادفی، در بسیاری از اوقات این دو را یکی در نظر می گیرند. لذا می توانیم فضای نمونه حاصل از انداختن یک تاس را همان مجموعه اعداد طبیعی 1 تا 6 در نظر بگیریم.

هر زیر مجموعه ای از فضای نمونه را یک پیشامد می نامیم (مجموعه تهی را هم شامل می شود).

در این حالت روشن است که تعداد پیشامدهای یک مجموعه با n عضو، 2ⁿ عدد خواهد بود.

بنا به تئوری بسامدی پوپر، احتمال عینی، یک تابع مجموعه ای است که به هر مجموعه پیشامد، عددی مابین صفر و یک را تخصیص میدهد که به آن عدد، احتمال وقوع آن پیشامد گفته می شود.

عدد احتمال عبارت است از حاصل تقسیم تعداد اعضای مجموعه پیشامد بر تعداد اعضای مجموعه فضای نمونه.

[math]P(E)=\frac{n(E)}{n(s)}[/math]

در رابطه فوق E مجموعه پیشامد و S فضای نمونه می باشد. n(E) و n(S) به ترتیب تعداد اعضای مجموعه پیشامد و تعداد اعضای فضای نمونه هستند. از رابطه (1) کاملا مشخص است که:

[math]{P(\phi)=0}\qquad{P(S)=1}\qquad{0}\leqq{P(E)}\leqq{1}[/math]

به عنوان مثال پیشامد آمدن عدد زوج در پرتاب تاس مجموعه ذیل می باشد:

[math]{E=\lbrace{2,4,6}\rbrace}[/math]

و فضای نمونه عبارت است از:

[math]{S=\lbrace{1,2,3,4,5,6}\rbrace}[/math]

داریم:

[math]{n(E)=3}\qquad{n(S)=6}[/math]

پس احتمال پیشامد آمدن عدد زوج در انداختن یک تاس عبارت است از:

[math]P(E)=\frac{3}{6}=0.5[/math]

بنا بر تفسیر تئوری بسامدی، گزاره “احتمال آمدن 5 در پرتاب بعدی تاس 1/6 است”، در واقع نه از پرتاب بعدی، بلکه از کل مجموعه پرتاب هایی خبر می دهد که پرتاب بعدی صرفا عضوی از آن است. مفاد این گزاره این است که بسامد نسبی آمدن عدد 5 در این مجموعه پرتاب ها برابر 1/6 است.

از ویژگی های مهم احتمالات عینی این است که پدیده های تصادفی که باعث آنها شده اند می توانند به هر چند بار که بخواهیم تکرار شوند. به بیان دیگر می توانیم آزمایش پرتاب تاس را با فرض مستقل بودن آزمایش ها از همدیگر به تعداد زیاد تکرار نماییم و تعداد دفعاتی را که تاس عدد 5 را نشان داده است بر کل تعداد دفعات پرتاب تقسیم کنیم. هر چه تعداد آزمایشات بیشتر باشد نسبت به دست آمده به 1/6 نزدیکتر خواهد بود.

پس مهمترین نکته در احتمالات عینی آزمایش پذیری و قابلیت صحت سنجی آنهاست.

حال به نوع دیگر احتمالات یعنی احتمالات ذهنی بپردازیم. من نام این نوع از احتمالات را احتمالات شناختی هم میگذارم. این نوع از احتمال از نزدیکی منطقی گزاره ها خبر می دهد. گزاره ها از نظر منطقی نسبت های گوناگونی از قبیل استنتاج پذیری، تضاد یا استقلال را نسبت به یکدیگر دارند. بنا بر تئوری ذهنی-منطقی که نماینده اصلی اش کینز می باشد، نسبت احتمال نیز نوعی نسبت منطقی میان گزاره هاست. استنتاج پذیری و تناقض دو حد نهایی نسبت احتمال اند.

اگر گزاره q نتیجه گزاره p باشد، گزاره p احتمال 1 را به q می دهد. و چنانچه p و q متناقض باشند، p به q احتمال صفر را می دهد. سایر نسبت های احتمال، بین این دو حد قرار می گیرند. یعنی هر چه مضمون q به p نزدیکتر باشد احتمال عددی گزاره q بیشتر خواهد شد.

کینز احتمال را درجه اعتقاد معقول می نامد. منظور از درجه اعتقاد معقول اعتماد ناشی از اطلاعات یا معرفت حاصل از گزاره p نسبت به گزاره q می باشد (گزاره p احتمالی را به گزاره q می دهد).

این چنین احتمالی صرفا با شناخت فرد تصمیم گیرنده و درجه باور وی به وقوع یک پدیده در ارتباط می باشد.

علیرغم احتمالات عینی که قابل اندازه گیری می باشند و اندازه آنها مستقل از ناظر است، احتمالات ذهنی کاملا با شرایط شناختی ناظر مرتبط هستند و می توانند از فردی به فرد دیگر به شدت متفاوت باشند.

قوانین ریاضی حاکم بر احتمالات ذهنی کاملا مشابه قوانین حاکم بر احتمالات عینی هستند. ولی این دو نوع احتمال بنیان متفاوتی از یکدیگر دارند. به دلیل ماهیت احتمالات ذهنی (یا همانگونه که ذکر شد، شناختی)، از این نوع از احتمال به وفور در علوم تصمیم گیری استفاده می شود.

مجددا یادآوری می شود که احتمالات ذهنی درجه باور فرد به یک موضوع (گزاره) می باشند، لذا کاملا وابسته به شخص هستند.

نکته مهم دیگر این است که پدیده هایی که منجر به احتمالات عینی می شوند تکرار پذیر هستند و در هر بار تکرار به یک نتیجه تصادفی متفاوت می رسند. لذا می توان آنها را ذاتا تصادفی دانست.

در حالیکه پدیده هایی که منجر به احتمالات ذهنی می شوند تکرارپذیر نمی باشند، و لذا ذاتا تصادفی هم نیستند بلکه ناآگاهی ما نسبت به آنها باعث می شود تا عدم قطعیت شناختی در موردشان داشته باشیم.

برای روشن شدن موضوع فرض نمایید که در یک مسیر خارج از شهر و در یک دشت به سمت یک آبادی روان هستید. راه را به درستی نمی شناسید، به یک سه راهی می رسید و در فکر هستید که کدام راه را انتخاب کنید تا شما را به مقصدتان برساند.

در اینجا موضوع انتخاب یک راه از میان سه راه موجود مطرح می باشد و به دلیل عدم شناخت شما، یک انتخاب تصادفی پیش روی شما قرار می گیرد. در صورتی که این مساله ذاتا تصادفی نیست، هیچ عامل شانسی هم در آن دخالت ندارد. برای اهالی محلی کاملا روشن است که کدام راه به کجا می رسد. چون شما دانش کافی ندارید موضوع برایتان تصادفی جلوه می کند. این پدیده یک احتمال ذهنی را نشان می دهد.

نکته بسیار مهم در خصوص احتمالات ذهنی نقش برجسته ای است که عامل اطلاعات بازی می کند. در احتمالات عینی، اطلاعات هیچ نقشی در برآورد احتمالات ندارد. به هنگام انداختن یک تاس احتمال آمدن عدد بعدی همواره یک ششم است، چه شما اطلاعات داشته باشید و چه اطلاعات نداشته باشید. در این حالت داشتن اطلاعات از تصادفی بودن نتیجه پرتاب بعدی تاس چیزی کم نمی کند.

در حالیکه در احتمالات شناختی، اطلاعات می تواند روی تابع توزیع احتمالات به شدت تاثیرگذار باشد. مثلا در خصوص انتخاب یک راه از میان سه راه ممکن، دسترسی به گوگل مپ می تواند به طور کامل عدم قطعیت و تصادفی بودن را منتفی نماید و با رساندن درجه آن به صفر، مساله را کاملا قطعی نماید.

یکی از راه هایی که می توان با کمک آن میزان عدم قطعیت در یک پدیده تصادفی ذهنی را اندازه گیری کرد استفاده از آنتروپی شانون است. آنتروپی شانون بسته به مقدار اطلاعات در دسترس قادر است میزان عدم قطعیت نهفته در یک تصمیم گیری احتمالی را اندازه گیری کند. در بخش بعدی مقاله به آنتروپی شانون می پردازیم.

2- آنتروپی شانون

فرض کنید مجموعه پیشامدهای حاصل از یک پدیده را با X و هر کدام از پیشامدها را با x نمایش دهیم

[math]{x}\in{X}[/math]

فرض کنید احتمال وقوع پیشامد x را با P(x) نشان دهیم. در اینصورت آنتروپی کل این مجموعه پیشامدها برابر خواهد بود با:

[math]{H(P(x)|}{x}\in{X)}=-{\sum\limits_{{x}\in{X}} {P(x)}{.log}_{2}{P(x)}}[/math]

تابع H اندازه ای است از مقدار عدم قطعیت در تابع توزیع. مثال زیر را در نظر بگیرید:

مجموعه X به صورت زیر تعریف شده است:

[math]X=\lbrace{X_{1},X_{2},X_{3},X_{4}}\rbrace[/math]

تابع توزیع احتمال روی اعضای این مجموعه عبارتند از:

(1-p) نشان می دهیم. اگر مقدار p را مابین صفر و یک تغییر دهیم به منحنی زیر خواهیم رسید:

[math]P=\lbrace{P_{1}=0.25,P_{2}=0.5,P_{3}=0.125,P_{4}=0.125}\rbrace[/math]

اندازه آنتروپی به صورت زیر روی مجموعه X محاسبه می شود:

[math]{H(P)}=-{0.25.log}_{2}{(0.25)}-{0.5.log}_{2}{(0.5)}-{0.125.log}_{2}{(0.125)}-{0.125.log}_{2}{(0.125)}[/math]

چه اتفاقی می افتاد اگر تابع توزیع فوق یکنواخت می بود، یعنی احتمال وقوع تمام مقادیر x برابر با 0.25 می شد؟

در این حالت مقدار آنتروپی برابر می شد با : H= 2

می توان نشان داد که این مقدار حداکثر مقدار آنتروپی برای یک توزیع با چهار ارزش می باشد.

حال فرض کنید پدیده تصادفی ما تنها دارای دو پیامد باشد. احتمال پیامد اول را با p و پیامد دوم را با q نشان می دهیم. اگر مقدار p را مابین صفر و یک تغییر دهیم به منحنی زیر خواهیم رسید:

[math]q={1-p}[/math]

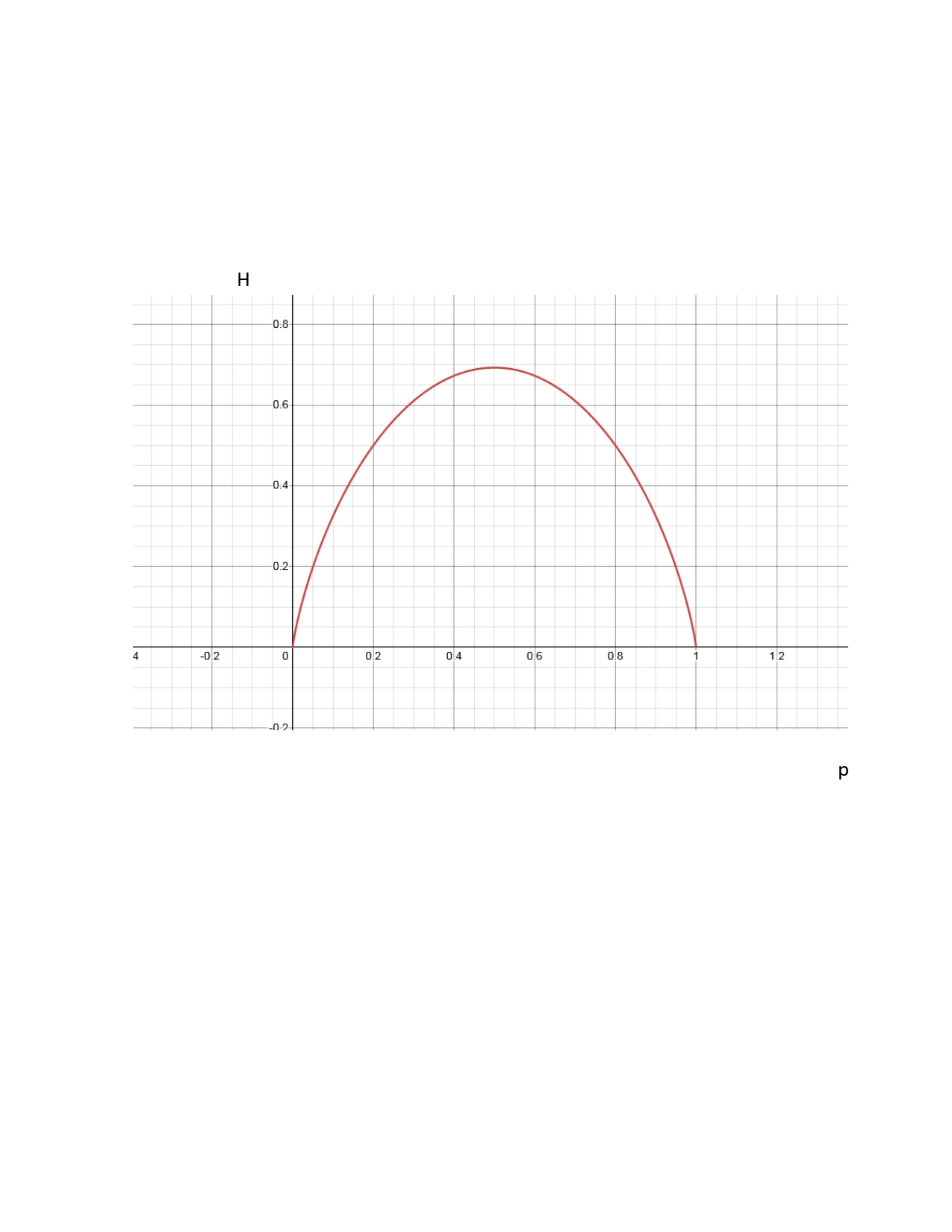
نکته جالب در این شکل این است که حداکثر آنتروپی زمانی به دست می آید که احتمالات برابر باشند. به بیان دیگر تصمیم گیرنده فاقد هر نوع اطلاعاتی در خصوص پدیده تصادفی است که با آن مواجه شده است. توجه دارید که تنها تابع توزیع احتمالی که در آن تمام احتمالات برابر می باشند توزیع یکنواخت است. یعنی در توزیع یکنواخت عدم قطعیت به حداکثر خود می رسد، به همین جهت هم آنتروپی حداکثر می باشد. اگر می خواهیم پدیده ای شناختی را با ماکزیمم عدم قطعیت ممکن مدلسازی نماییم، باید از تابع چگالی یکنواخت استفاده کنیم.

حال به سراغ بخش بعدی این مقاله می رویم، یعنی رابطه مابین احتمالات و امکان یا به بیان دیگر رابطه احتمال و امکان. این بخش برای درک چرایی استفاده وسیع از اعداد فازی مثلثی ضروری است.

3- تبدیلات احتمالات و امکان

بدون آنکه بخواهیم وارد جزییات شویم این نکته را می پذیریم که درجه امکان یک حد بالا روی درجه احتمال می باشد. در یک مقاله دیگر صرفا روی این موضوع بحث خواهم کرد ولی فعلا آنرا به همین شکل قبول می کنیم.

یکی از موارد جالب در تئوری امکان و احتمال، تبدیل اندازه احتمال به اندازه امکان می باشد. می توان اندازه احتمال را به امکان تبدیل نمود ولی این امر با از دست دادن اطلاعات همراه خواهد بود. عکس موضوع هنگامی صادق است که اطلاعات جدید به سیستم تزریق نماییم. به همین دلیل نیز معمولا حالت اول بیشتر رایج می باشد.

هر نوع تبدیلی از این دست بایستی توسط یک اصل خاص اطلاعاتی پشتیبانی گردد. اصل اول عبارت است از:

در تبدیل امکان به احتمال بایستی خاصیت وجود عدم قطعیت انتخاب بین خروجی ها حفظ گردد. در عین حال تقارن مساله در صورت وجود نیز باید حفظ شود.

اصل دوم عبارت است از:

در تبدیل احتمال به امکان بایستی توزیع امکان با بیشترین مقدار اطلاعات تحت محدودیت های اصل سازگاری امکان/احتمال به دست آید.

اصل سازگاری اصلی است که توسط دکتر لطف اله عسگری زاده بیان شده است و بر طبق آن یک پدیده در ابتدا باید ممکن باشد تا بتواند محتمل گردد. طبق این اصل درجه امکان جد بالا روی درجه احتمال می باشد. این اصل ایجاب می کند که یک پیشامد می باید پیش از محتمل بودن، ممکن باشد. لذا درجات امکان هر چه که باشند، نمی توانند کمتر از درجات احتمال باشند.

یکی از روش هایی که برای تبدیل احتمال به امکان توسعه یافته است روش Klir می باشد که بر مبنای عدم تغییر اطلاعات قرار دارد. یکی دیگر از روش های توسعه داده شده در این زمینه توسط

 Dubois & Prade پیشنهاد شده است. به دلیل موضوع بحث در این مقاله، روش Dubois & Prade را برای صرفا حالت خاص توابع چگالی احتمال متقارن پیوسته و unimodal در نظر خواهم گرفت. بدیهی است که این روش شامل حالت های دیگر هم می گردد.

باز هم بدون ورود به جزییات ریاضی قضیه زیر را می پذیریم:

قضیه1) یک فرم بسته توزیع امکان براساس بازه های اطمینان حول نمای

یک توزیع یکنواخت در بازه دو حد a و b را در نظر بگیرید:

[math]x^{*}=x^{m}[/math]

برای چگالی های احتمال پیوسته Unimodal که در سمت چپ x^m کاملا صعودی و در سمت راست x^m کاملا نزولی می باشند به صورت زیر به دست می آید:

[math]\forall {x}\in{[-\infty,x^{m}],}\qquad {{\pi}^{x^{m}}{(x)}}={{\pi}}^{x^{m}}{(2x^{m}-{x)}}={1-P([x, 2x^{m}-x])}[/math]

حال اجازه دهید با استفاده از قضیه فوق ببینیم توزیع امکان یک تابع توزیع احتمال یکنواخت چه خواهد بود. یک توزیع یکنواخت در بازه دو حد a و b را در نظر بگیرید:

[math]{P(x)}=\frac{x-a}{b-a}[/math]

[math]x^{m}=\frac{a+b}{2}[/math]

 با اعمال قضیه 1 بر این توزیع یکنواخت به قضیه 2 خواهیم رسید.

قضیه 2) تابع توزیع امکان تبدیل یافته تابع توزیع احتمال یکنواخت روی یک بازه بسته [a,b] حول x^m

یک توزیع امکان مثلثی است با نمای x^m که پشتیبان آن همان بازه [a,b] می باشد.

به بیان دیگر اگر شما با توزیع احتمال یکنواخت سروکار داشته باشید، توزیع امکان تبدیل یافته آن یک عدد فازی مثلثی با همان بازه و همان نما خواهد بود.

این امر کاملا توضیح می دهد که چرا اعداد فازی مثلثی اینچنین پر کاربرد هستند. در مسائل دنیای واقعی، تصمیم گیرنده در اکثر مواقع هیچ نوع اطلاعاتی در خصوص تابع توزیع احتمال پدیده تصادفی که با آن مواجه است ندارد. لذا بهترین انتخاب برای وی تابع توزیع یکنواخت با حداکثر عدم قطعیت می باشد. با تبدیل این تابع توزیع احتمال به توزیع امکان، طبیعی است که به عدد فازی مثلثی خواهیم رسید.