فاصله بین دو عدد فازی را می‌توان با استفاده از اندازه های فاصله فازی گوناگونی تعریف کرد که هدف تمامی آنها کمی سازی “اختلاف” بین مجموعه‌های فازی است که این اعداد نماینده شان می باشند. این فواصل اغلب منجر به یک عدد فازی به عنوان خود فاصله می‌شود، اگرچه فاصله های غیر فازی نیز وجود دارند. در این زمینه رویکردهای متعددی پیشنهاد شده اند، از جمله روش های مبتنی بر انتگرال، روش هایی که از برش‌ آلفا استفاده می‌کنند، و نیز رویکردهایی که مبتنی بر اصل توسعه یا فاصله هاسدورف هستند.

از معروف ترین روش های موجود می توان به روش Voxman ، روش Chakraborty & Chakraborty ، عباس بندی و حاجی قاسمی، سعدی نژاد، بیگی و همکاران، حسامیان، Chen & Wang و تعداد بسیار زیاد دیگر روش ها اشاره نمود.

در این نوشتار روش Voxman را که از روش های اولیه و پایه ای می باشد توضیح خواهم داد. البته به خوانندگان علاقمند توصیه می کنم که حتما روشهای دیگر را نیز مطالعه نمایند.

روش Voxman

فاصله فازی Voxman یکی از روش های پایه ای برای محاسبه فاصله مابین دو عدد فازی است. این روش از مفهوم برش‌ آلفا برای نمایش اعداد فازی استفاده می‌کند و سپس فاصله را بر اساس اختلاف بین نقاط انتهایی چپ و راست این برش‌های آلفا تعیین می‌نماید.

اگر تابع عضویت یک عدد فازی را در نظر بگیریم، برش آلفای این عدد فازی، یک بازه قطعی است که شامل تمام عناصری با مقدار عضویت بزرگتر یا مساوی یک مقدار آلفای خاص (بین 0 و 1) است. به عنوان مثال، اعداد فازی A و B را در نظر بگیرید. برش آلفای این اعداد بازه ای قطعی از مقادیر پشتیبان این اعداد می باشد.

رابطه (1)

[math]{A}_{\alpha}={[}{A}_{L}{(\alpha)}{,}{{A}_{R}{(\alpha)}}{]}=\{{x}\in{X}\vert\quad{\mu}_{A}{(x)}\geq{\alpha}\qquad{0}\leq{\alpha}\leq{1}\}[/math]

رابطه (2)

[math]{B}_{\alpha}={[}{B}_{L}{(\alpha)}{,}{{B}_{R}{(\alpha)}}{]}=\{{x}\in{X}\vert\quad{\mu}_{B}{(x)}\geq{\alpha}\qquad{0}\leq{\alpha}\leq{1}\}[/math]

فاصله Voxman در حقیقت یک مجموعه فازی می باشد که با برش آلفای خود قابل تعریف است.

رابطه (3)

[math]{d}_{voxman}{(A,B)}={[L(\alpha),R(\alpha)]}[/math]

داریم:

رابطه (4)

[math]{L(\alpha)}={max\{}{B}_{L}{(\alpha)}{-}{A}_{R}{(\alpha)}{,}{0}\}\qquad{if}\qquad\frac{{A}_{L}{(1)}+{A}_{R}{(1)}}{2}\leq\frac{{B}_{L}{(1)}+{B}_{R}{(1)}}{2}[/math]

رابطه (5)

[math]{L(\alpha)}={max\{}{A}_{L}{(\alpha)}{-}{B}_{R}{(\alpha)}{,}{0}\}\qquad{if}\qquad\frac{{B}_{L}{(1)}+{B}_{R}{(1)}}{2}{<}\frac{{A}_{L}{(1)}+{A}_{R}{(1)}}{2}[/math]

رابطه (6)

[math]{R(}{\alpha)}={max}\{{A}_{R}{(\alpha)}{-}{B}_{L}{(\alpha)}{,}\quad{B}_{R}{(\alpha)}{-}{A}_{L}{(\alpha)}\}[/math]

فاصله به دست آمده نیز یک عدد فازی است که نمایش برش آلفای آن توسط فرمول‌های بالا تعریف می‌شود. این بدان معناست که فاصله بین دو عدد فازی یک مقدار قطعی نیست، بلکه یک نمایش فازی از فاصله است که منعکس کننده عدم قطعیت ذاتی موجود در خود اعداد فازی می باشد.

رویکرد voxman اساساً برش‌های آلفای متناظر با دو عدد فازی را مقایسه می‌کند. مؤلفه‌ی L(α) همپوشانی یا جدایی “چپ” بین برش‌های آلفا را تعیین می‌کند، در حالی که R(α) همپوشانی یا جدایی “راست” را ثبت می‌کند. فاصله‌ دو عدد فازی، یک عدد فازی است که نشان دهنده‌ی میزان جدایی یا همپوشانی دو عدد فازی می باشد.

مثال عددی

دو عدد فازی ذوذنقه ای را به شکل زیر در نظر بگیرید:

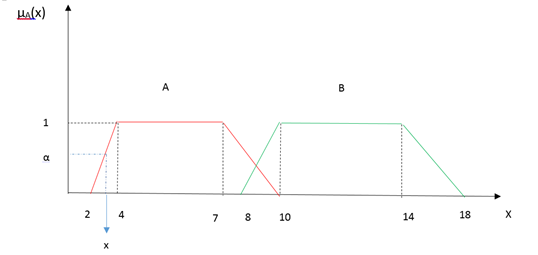
اعداد فازی عبارتند از:

[math]{A}={(2,4,7,8)}[/math]

[math]{B}={(8,10,14,18)}[/math]

حال حدود چپ و راست برش آلفا را برای این دو عدد به دست خواهیم آورد. مثلا عدد فازی A را در نظر بگیرید. حد چپ برش آلفا برحسب پارامتر آلفا عبارت است از:

[math]\frac{x-2}{4-2}=\frac{\alpha}{1}\qquad\Rightarrow\qquad{x=}{2}\alpha{+2}[/math]

به همین ترتیب برای حد راست برش آلفای عدد A برحسب پارامتر آلفا داریم:

[math]{x=}{10-}{3}\alpha[/math]

لذا خواهیم داشت:

[math]{A}_{\alpha}={[2\alpha+2,10-3\alpha]}[/math]

به همین ترتیب برای عدد فازی ذوذنقه ای B هم خواهیم داشت:

[math]{B}_{\alpha}={[2\alpha+8,18-4\alpha]}[/math]

حال برای تعیین اینکه L(α) از رابطه 4 پیروی می کند یا رابطه 5، نامساوی مربوطه را بررسی می نماییم.

[math]\frac{{A}_{L}{(1)}+{A}_{R}{(1)}}{2}\leq\frac{{B}_{L}{(1)}+{B}_{R}{(1)}}{2}[/math]

[math]\frac{4+7}{2}\leq\frac{10+14}{2}\Rightarrow\frac{11}{2}\leq\frac{24}{2}[/math]

که به معنای صادق بودن رابطه 4 می باشد.

[math]{L(\alpha)}={max\{}{B}_{L}{(\alpha)}{-}{A}_{R}{(\alpha)}{,}{0}\}[/math]

[math]{L(\alpha)}={max\{}{(2\alpha+8)-(10-3\alpha)}{,}{0}\}={max}{\{5\alpha-2,0\}}[/math]

و برای R(α) هم خواهیم داشت:

[math]{R(}{\alpha)}={max}\{{A}_{R}{(\alpha)}{-}{B}_{L}{(\alpha)}{,}\quad{B}_{R}{(\alpha)}{-}{A}_{L}{(\alpha)}\}[/math]

[math]{max}{\{2-5\alpha,16-6\alpha\}}[/math]

به عنوان مثال فرض کنید α=0.5 در نظر گرفته شود. در این صورت فاصله وکسمن دو عدد ذوذنقه ای فوق عبارت خواهد شد از یک عدد فازی که سمت چپ و راست برش آلفای آن برابر است با:

[math]{d}_{voxman}{(A,B)}={[L(\alpha),R(\alpha)]}={[0.5,13]}[/math]

طبیعی است که برای کاربردهای عملی می توان به عنوان مثال از میانگین این بازه استفاده نمود.