پی یر بزیه (Pierre Bezier, 1910-1999) مهندس فرانسوی، در سال 1960 میلادی برای طراحی خطوط انحنای خودرو های رنو منحنی های بزیه را ابداع نمود. منحنی بزیه یک منحنی پارامتری است که در حال حاضر در گرافیک و انیمیشن های کامپیوتری کاربرد گسترده ای را دارد. مجموعه ای از نقاط گسسته که به آنها نقاط کنترل گفته می شود، منحنی بزیه را تعریف می کنند. در حالت توسعه یافته، می توان صفحات بزیه را نیز به دست آورد.

در این مقاله روش بزیه برای به دست آوردن معادلات منحنی بزیه از تعدادی نقاط کنترل مورد بحث قرار خواهد گرفت. لازم به ذکر است که منحنی بزیه از تمام نقاط کنترلی عبور نمی کند بلکه این نقاط یک پوشش برای آن فراهم می نمایند. در این مقاله روش به دست آوردن معادله منحنی بزیه بر اساس نقاط کنترلی داده شده ارائه خواهد گردید.

تعریف: یک منحنی بزیه دارای n+1 نقطه کنترلی می باشد.

[math]{C}_{k}\triangleq{{(C}_{0}{,}{C}_{1}{,}{…,}{C}_{n}{)}}\qquad\qquad{(1)}[/math]

که به صورت زیر تعریف می گردند:

[math]{f(t,n,c)}\triangleq\sum\limits_{k=0}^{n}{C}_{k}{B}_{n,k}{(t)}\qquad\qquad{(2)}[/math]

به B_n,k(t) چند جمله ای برنشتاین گفته می شود و مقدار آن به صورت زیر قابل محاسبه است.

[math]{B}_{n,k}{(t)}=\begin{pmatrix}n\\k\end{pmatrix}{(1-t)}^{(n-k)}{t}^{k}\qquad{t}\in{[0 , 1]}\qquad\qquad{(3)}[/math]

[math]{C}_{k}\triangleq{{(x}_{k}{,y}_{k}{)}}^{T}\qquad\qquad{(4)}[/math]

(علامت T به معنای ترانسپوز یا ترانهاده می باشد)

در عین حال داریم:

[math]{f(t,n,c)}\in\Re^{2}\qquad\qquad{(5)}[/math]

[math]{f(t,n,c)}={{[f}_{x}{(t,n,}{C}_{x}{),}{f}_{y}{(t,n,}{C}_{y}{)]}}^{T}\qquad\qquad{(6)}[/math]

که در آن داریم:

[math]{(C}_{x}{,C}_{y}{)}\triangleq{{[(x}_{0}{,y}_{0}{)}{,(x}_{1}{,y}_{1}{)},{…},{(x}_{n}{,y}_{n}{)]}}^{T}\qquad\qquad{(7)}[/math]

برخی از ویژگی های مهم منحنی بزیه عبارتند از:

1- منحنی بزیه f(t,n,c) یک چند ضلعی محدب است که گوشه های آن نقاط کنترلی C₀, C₁, C₂, …,C_n می باشند (در حقیقت یک convex hull را تشکیل می دهند).

2- داریم:

[math]{max}_{t}\quad{B}_{n,k}{(t)}\Rightarrow{t}^{*}=\frac{k}{n}\qquad\qquad{(8)}[/math]

3- داریم:

[math]{f(0,n,c)}={C}_{0}\\{f(1,n,c)}={C}_{n}\qquad\qquad{(9)}[/math]

حال می توانیم به جزییات منحنی های بزیه بپردازیم. ابتدا منحنی درجه دوم بزیه را در نظر می گیریم.

سه نقطه P₀, P₁, P₂ را در نظر بگیرید. می خواهیم یک منحنی درجه دوم بزیه را به کمک این سه نقطه ترسیم کنیم. منحنی درجه دوم بزیه مسیری است که توسط تابع B(T) ترسیم می گردد. شکل 1 این مفهوم را نشان می دهد.

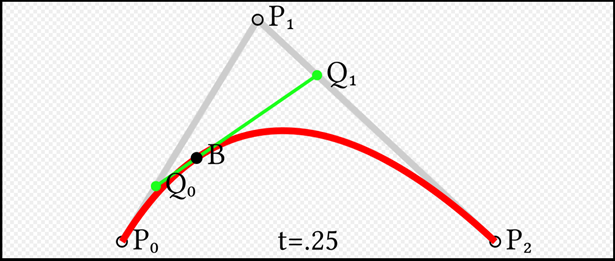
شکل 1- منحنی بزیه با سه نقطه کنترلی و مثالی از t=0.25

با استفاده از روابط (1) تا (7) می توانیم روابط ذیل را برای حالت با سه نقطه کنترل بنویسیم.

[math]{B(t)}={(1-t)[(1-t)}{P}_{0}+{t}{P}_{1}{]}+{t[(1-t)}{P}_{1}+{t}{P}_{2}{]}\qquad{(0}\leq{t}\leq{1)}\qquad\qquad{(10)}[/math]

[math]{B(t)}={(1-t)}^{2}{P}_{0}+{2(1-t)t}{P}_{1}+{t}^{2}{P}_{2}\qquad{(0}\leq{t}\leq{1)}\qquad\qquad{(11)}[/math]

[math]{B(t)}={P}_{1}+{(1-t)}^{2}{(}{P}_{0}-{P}_{1}{)}+{t}^{2}{(}{P}_{2}-{P}_{1}{)}\qquad{(0}\leq{t}\leq{1)}\qquad\qquad{(12)}[/math]

مشتق اول B(t) نسبت به t عبارت است از:

[math]{B}^\prime{(t)}={2(1-t)(}{P}_{1}-{P}_{0}{)}+{2t(}{P}_{2}-{P}_{1}{)}\qquad{(0}\leq{t}\leq{1)}\qquad\qquad{(13)}[/math]

مشتق دوم B(t) نسبت به t عبارت است از:

[math]{B}^{”}{(t)}={2(}{P}_{2}-{P}_{1}+{P}_{0}{)}\qquad\qquad{(14)}[/math]

حال منحنی های مکعب بزیه را در نظر می گیریم. چهار نقطه کنترلی P0, P1, P2, P3 را داریم. می توان منحنی مکعب بزیه را ترکیبی از دو منحنی درجه دوم هم در نظر گرفت. شکل 2 این مفهوم را نمایش می دهد.

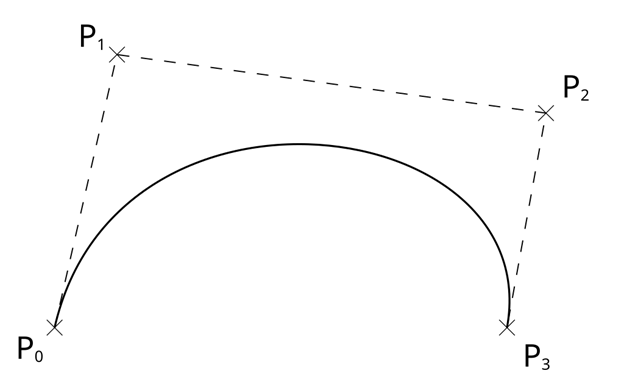
شکل 2- منحنی بزیه با چهار نقطه کنترلی

[math]{B(t)}={(1-t)}{B}_{{P}_{0}{,}{P}_{1}{,}{P}_{2}}{(t)}+{t}{B}_{{P}_{1}{,}{P}_{2}{,}{P}_{3}}{(t)}\qquad{0}\leq{t}\leq{1}\qquad\qquad{(15)}[/math]

[math]{B(t)}={(1-t)}^{3}{P}_{0}+{3}{(1-t)}^{2}{t}{P}_{1}+{3}{(1-t)}{t}^{2}{P}_{2}+{t}^{3}{P}_{3}\qquad{0}\leq{t}\leq{1}\qquad\qquad{(16)}[/math]

فرمول عمومی بزیه برای B_P0P1…Pn عبارت است از:

[math]{B}{(t)}=\sum\limits_{i=0}^{n}\begin{pmatrix}n\\i\end{pmatrix}{(1-t)}^{(n-i)}{t}^{i}{P}_{i}\qquad\qquad\qquad{(17)}[/math]

[math]{B(t)}={(1-t)}^{n}{P}_{0}+\begin{pmatrix}n\\1\end{pmatrix}{(1-t)}^{(n-1)}{P}_{1}{t}+{…}+\begin{pmatrix}n\\n-1\end{pmatrix}{(1-t)}{P}_{n-1}{t}^{(n-1)}+{t}^{n}{P}_{n}\qquad{0}\leq{t}\leq{1}\qquad\qquad{(18)}[/math]

حال مثالی را در نظر می گیریم. مجموعه نقاط x از 6 مقدار تشکیل شده است.

[math]{X}=\lbrace{1,2,3,4,5,6}\rbrace[/math]

نقاط کنترلی برحسب مختصات (x,y) به صورت زیر داده شده است.

[math]{(P}_{0}{)}{:}{y(x=1)}={0,}\quad{(P}_{1}{)}{:}{y(x=2)}={0.5,}\quad{(P}_{2}{)}{:}{y(x=6)}={0}[/math]

[math]{B(t)}=\begin{pmatrix}2\\0.5\end{pmatrix}+{(1-t)}^2\biggl[\begin{pmatrix}1\\0\end{pmatrix}-\begin{pmatrix}2\\0.5\end{pmatrix}\biggr]+{t}^2\biggl[\begin{pmatrix}6\\0\end{pmatrix}-\begin{pmatrix}2\\0.5\end{pmatrix}\biggr][/math]

با تغییر متغیر t مابین صفر و یک می توانیم نقاط روی منحنی بزیه با مختصات (x,y) را به دست آوریم. معادله منحنی بزیه برای سه نقطه کنترلی به صورت زیر خواهد بود.

[math]{B(t)}=\begin{pmatrix}2-(1-t)^2+4t^2\\0.5-0.5(1-t)^2-0.5t^2\end{pmatrix}[/math]

[math]{x}={2}-{(1-t)}^{2}+{4}{t}^{2}[/math]

[math]{y}={0.5}-{0.5}{(1-t)}^{2}-{0.5}{t}^{2}[/math]

با تغییر مقادیر t مابین صفر و یک شکل ذیل را خواهیم داشت. در این شکل نقاط P₀, P₁, P₂ نقاط کنترلی می باشند. معادله منحنی به صورت تابعی از متغیر t داده می شود که با تغییر مقدار آن بین صفر و یک، هر نقطه منحنی به صورت یک زوج مرتب x(t), y(t) داده می شود. شکل 3 منحنی بزیه و نقاط کنترلی را برای این مثال نشان می دهد.

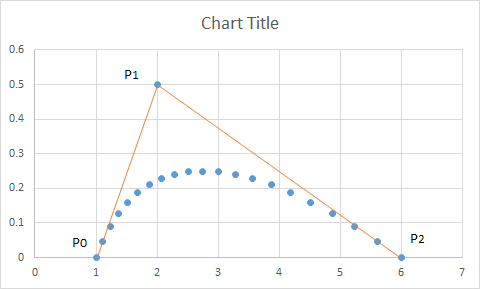
شکل 3- منحنی بزیه و نقاط کنترلی برای مثال داده شده

از ویژگی های منحنی بزیه این است که متناسب با موقعیت قرار گیری نقاط کنترلی، می تواند منحنی های غیر محدب را نیز ایجاد نماید.