در بسیاری از مباحث مهندسی صنایع و دیگر شاخه های مهندسی، نیاز به مقایسه و محاسبه فاصله میان دو یا چند تابع توزیع احتمال وجود دارد. یکی از این موارد، تصمیم گیری و بخصوص تصمیم گیری چند معیاره می باشد. تصور کنید که یک یا چند معیار دارای عدم قطعیت تصادفی بوده و از توابع توزیع احتمال گسسته یا پیوسته پیروی می نمایند. طبعا یکی از اقدامات اساسی برای حل، مقایسه معیارها برای هر زوج گزینه خواهد بود. حال چگونه بایستی توابع توزیع احتمال برای یک معیار را در یک زوج گزینه با هم مقایسه کرد؟

مثلا تصور کنید معیار مورد بحث معیار قیمت است و می دانیم که از توزیع نرمال پیروی میکند. برای گزینه A1 تابع توزیع قیمت به صورت N(50,6) و برای گزینه A2 این توزیع به صورت N(46,8) می باشد، حال چگونه بایستی این دو تابع توزیع با هم مقایسه گردند؟

به دلیل اهمیت موضوع، در این بخش پس از ارائه توضیحات کلی در خصوص روش های گوناگون اندازه گیری فاصله توابع توزیع احتمال، روی سه روش متمرکز خواهم شد. ابتدا روش کولبک – لیبلر توضیح داده خواهد شد و سپس به روش TVD خواهم پرداخت. روش کولبک – لیبلر این قابلیت را دارد که هم برای توابع توزیع پیوسته و هم برای توابع توزیع گسسته به کار برده شود، ولی توصیه من این است که آنرا برای توابع توزیع گسسته به کار ببرید.

سپس روش TVD را توضیح خواهم داد و آنرا به خصوص برای دو تابع توزیع احتمال پیوسته پر کاربرد یعنی توزیع یکنواخت و توزیع نرمال (با واریانس برابر) برایتان شرح می دهم.

سومین روش، فاصله هلینگر می باشد که کاربرد ساده تری برای طیف بزرگتری از توابع توزیع احتمال گسسته و پیوسته دارد (از جمله توزیع های نرمال با واریانس های نابرابر)

حال به کلیاتی در خصوص روش های مختلف اندازه گیری فاصله توابع توزیع احتمال خواهیم پرداخت.

1- کلیات

فاصله مابین دو توزیع احتمال را می‌توان با استفاده از فواصل آماری مختلف، که هر کدام دیدگاه منحصر به فردی در مورد عدم تشابه ارائه می‌دهند، کمّی نمود. این معیارها به ارزیابی میزان تفاوت دو توزیع احتمال کمک می‌کنند، که برخی از نمونه‌های رایج آن شامل فاصله کل تغییرات (TVD)، واگرایی کولبک-لیبلر  (Kullback-Leibler)، فاصله هلینگر (Hellinger) و فاصله واسرشتاین (Wasserstein) است.

برخی مفاهیم اصلی در ذیل توضیح داده شده اند.

1-1- فاصله آماری (Statistical Distance)

 فاصله آماری، تفاوت بین دو شیء آماری، همانند توزیع‌های احتمال یا نمونه‌های حاصل از جمعیت  را کمّی می‌کند. این فواصل را می‌توان برای مقایسه در موارد زیر استفاده کرد:

– دو توزیع احتمال

– نمونه‌هایی از جمعیت‌های مختلف

– ملاحظات منفرد (نقطه ای) از یک توزیع یا نمونه تصادفی

 2-1- فاصله کل تغییرات (TVD: Total Variation Distance)

– فاصله کل تغییرات (یا فاصله آماری) معیاری برای سنجش میزان متفاوت بودن دو توزیع احتمال می باشد

– این فاصله عبارت است از نصف انتگرال قدر مطلق تفاوت بین توابع چگالی احتمال (PDF) دو تابع توزیع

– TVD حداکثر اختلاف در احتمال وقوع هر پیشامدی تحت دو توزیع احتمال مورد نظر را اندازه‌گیری می‌کند

 3-1- واگرایی کولبک-لیبلر (KL)

– واگرایی KL، که به عنوان آنتروپی نسبی نیز شناخته می‌شود، دست آورد اطلاعات را هنگام تقریب یک توزیع احتمال با توزیع دیگر اندازه‌گیری می‌کند

– اغلب برای مقایسه میزان خوب بودن مدل‌سازی یک توزیع توسط توزیع دیگر استفاده می‌شود

– واگرایی KL نامتقارن است، به این معنی که واگرایی KL از P به Q لزوماً با واگرایی از Q به P یکسان نیست

 4-1- فاصله واسرشتاین

– فاصله واسرشتاین، معیاری برای مقایسه توابع توزیع‌ احتمال می باشد

– این معیار، حداقل “هزینه” تبدیل یک توزیع به توزیع دیگر را با در نظر گرفتن هزینه جابجایی “جرم” مابین مکان‌ها نشان می‌دهد

– این فاصله به ویژه هنگامی موثر است که توابع توزیع‌ مورد مقایسه، دامنه پشتیبان متفاوتی دارند یا با استفاده از معیارهای دیگر به راحتی قابل مقایسه نیستند

 5-1- حداکثر اختلاف میانگین (MMD: Maximum Mean Discrepancy)

 – MMD از یک تابع کرنل برای نگاشت توزیع‌های احتمال به یک فضای ویژگی با ابعاد بالاتر استفاده می‌کند و سپس فاصله بین میانگین‌ها را در آن فضا اندازه‌گیری می نماید

6-1- فاصله باتاچاریا (Bhattacharyya)

این فاصله بر اساس ضریب باتاچاریا قرار دارد و میزان شباهت بین دو توزیع احتمال را اندازه‌گیری می‌کند

7-1- فاصله هلینگر (Hellinger)

– معیار دیگری برای مقایسه توزیع‌های احتمال می باشد و بر اساس فاصله باتاچاریا قرار دارد

8-1- واگرایی χ²

– این واگرایی تفاوت بین دو توزیع احتمال را اندازه‌گیری می‌کند، به‌ویژه زمانی که یک توزیع بر دیگری غالب باشد

9-1- فاصله‌های L1 و L2

– این‌ها معیارهای فاصله ساده‌ای هستند که می‌توانند با مقایسه مقادیر توزیع‌های احتمال در نقاط خاص محاسبه شوند.

2- فاصله (واگرایی) کولبک – لیبلر

واگرایی کولبک-لیبلر معیاری است جهت اندازه گیری واگرایی یک توزیع احتمال از یک توزیع احتمال ثانویه. مقدار صفر این معیار به معنای آن است که می توانیم انتظار رفتار مشابه (و نه دقیقا یکسان) از دو توزیع را داشته باشیم. در حالیکه مقدار یک نشان می دهد که دو نوع توزیع دارای رفتار متضادی هستند.

مقدار واگرایی KL توزیع Q نسبت به توزیع P اغلب به صورت زیر نشان داده می شود:

[math]{D}_{KL}{(P}\parallel{Q)}[/math]

در حوزه اطلاعات، از این معیار به عنوان بهره اطلاعاتی حاصله به شرطی که به جای توزیع P از توزیع Q استفاده شود، یاد می شود.

از منظر استنتاج بیزین، واگرایی KL توزیع Q نسبت به توزیع P ، یک معیار اندازه گیری برای اطلاعات کسب شده به هنگامی است که یک اصلاح باورها از توزیع پیشین احتمالی Q به توزیع پسین احتمالی P رخ دهد. یعنی مقداری از اطلاعات است که به واسطه تقریب زدن P در هنگامی که از Q برای آن استفاده می شود مورد نیاز است. برای توابع توزیع احتمال گسسته، مقدار D_KL به صورت زیر قابل محاسبه است (رابطه 1).

[math]{D}_{KL}{(P}\parallel{Q)}=\sum\limits_{i}{P}_{i}{log}\frac{{P}_{i}}{{Q}_{i}}[/math]

در حالت توابع توزیع احتمال پیوسته هم خواهیم داشت (رابطه 2):

[math]{D}_{KL}{(P}\parallel{Q)}=\int\limits_{-\infty}^{+\infty}{P(x)}{log}\frac{{P(x)}}{{Q(x)}}{dx}[/math]

حال اجازه دهید تا با دو مثال برای توابع توزیع گسسته عملکرد معیار واگرایی KL روشن شود.

مثال 1) متغیر تصادفی X را در نظر بگیرید. این متغیر تصادفی می تواند چهار مقدار {1،2،3،4} را اختیار نماید. تابع توزیع Q(x) را یک تابع یکنواخت فرض میکنیم. تابع توزیع P(x) مطابق جدول (1) داده شده است. می خواهیم مقدار واگرایی KL این دو تابع توزیع را از همدیگر محاسبه کنیم.

4	3	2	1	x
1/4	1/4	1/4	1/4	Q(x)
1/12	1/3	1/3	1/4	P(x)

حال واگرایی این دو تابع توزیع را از همدیگر محاسبه می نماییم.

[math]{D}_{KL}{(P}\parallel{Q)}=\frac{1}{4}{log}\frac{\frac{1}{4}}{\frac{1}{4}}+\frac{1}{3}{log}\frac{\frac{1}{3}}{\frac{1}{4}}+\frac{1}{3}{log}\frac{\frac{1}{3}}{\frac{1}{4}}+\frac{1}{12}{log}\frac{\frac{1}{12}}{\frac{1}{4}}={0.0435}[/math]

یعنی در بازه بین صفر و یک، واگرایی توزیع P در جدول (1) نسبت به یک توزیع پیش فرض یکنواخت، 0.0435 می باشد.

حال یک تابع توزیع دیگر را در نظر بگیرید که به تابع توزیع یکنواخت نزدیکتر می باشد و در جدول (2) نشان داده شده است.

4	3	2	1	x
1/4	1/4	1/4	1/4	Q(x)
1/5	3/10	3/10	1/5	P(x)

مجددا مقدار واگرایی دو تابع توزیع را از همدیگر محاسبه می کنیم. خواهیم داشت:

[math]{D}_{KL}{(P}\parallel{Q)}=\frac{1}{5}{log}\frac{\frac{1}{5}}{\frac{1}{4}}+\frac{3}{10}{log}\frac{\frac{3}{10}}{\frac{1}{4}}+\frac{3}{10}{log}\frac{\frac{3}{10}}{\frac{1}{4}}+\frac{1}{5}{log}\frac{\frac{1}{5}}{\frac{1}{4}}={0.00874}[/math]

ملاحظه می گردد که مقدار واگرایی KL برای تابع توزیع جدول (2) از توزیع یکنواخت، به عدد صفر نزدیکتر می باشد تا تابع توزیع مربوط به جدول (1).

3- فاصله کل تغییرات (TVD)

TVD بزرگترین اختلاف مطلق بین احتمالاتی است که دو توزیع احتمال به یک رویداد واحد A نسبت می‌دهند. فاصله کل تغییرات مابین دو تابع توزیع P و Q را به صورت ذیل نشان می دهیم:

[math]\delta{(P,Q)}={Sup}_{{A}\in{F}}\vert{P(A)-Q(A)\vert}[/math]

معمولا TVD را نصف فاصله L1 دو تابع توزیع در نظر می گیرند. برای توابع گسسته داریم:

[math]\delta{(P,Q)}=\frac{1}{2}\sum_{x}{\vert(P(x)-Q(x)\vert}[/math]

برای توابع پیوسته خواهیم داشت:

[math]\delta{(P,Q)}=\frac{1}{2}\int_{x}{\vert(P(x)-Q(x)\vert}{dx}[/math]

در حقیقت TVD نصف مساحت بین دو منحنی می باشد. در شکل 1 این مقدار برابر با نصف ناحیه تیره رنگ می باشد.

شکل 1- ناحیه مابین دو منحنی

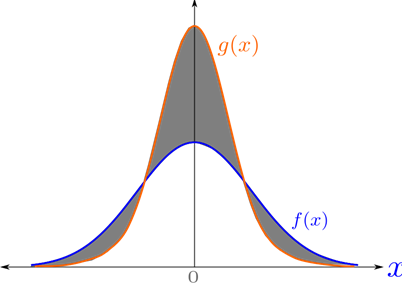
رابطه جالبی مابین TVD و KL به صورت ذیل وجود دارد:

[math]\delta{(P,Q)}\leq\sqrt{\frac{1}{2}{D}_{KL}{(P}\Vert{Q)}}[/math]

از آنجاییکه محاسبه مستقیم TVD چندان ساده نمی باشد، برای دو تابع توزیع پیوسته یکنواخت و نرمال روش های ذیل ارائه می گردند.

3-1- محاسبه TVD برای دو تابع توزیع یکنواخت

فرض کنید دو تابع توزیع یکنواخت A و B را به صورت ذیل داشته باشیم.

[math]{A}={[a,b]}[/math]

[math]{B}={[c,d]}[/math]

مقدار TVD از رابطه ذیل قابل محاسبه می باشد.

[math]{TVD}={1-}\frac{min(b,d)-max(a,c)}{(b-a)+(d-c)}[/math]

به عنوان مثال دو تابع توزیع یکنواخت زیر را در نظر بگیرید:

[math]{A}={[2,6]}\qquad{B}={[4,10]}[/math]

[math]{TVD}={1-}\frac{min(6,10)-max(2,4)}{(6-2)+(10-4)}={0.8}[/math]

2-3- محاسبه TVD برای دو تابع توزیع نرمال با واریانس برابر

دو تابع توزیع نرمال با میانگین های متفاوت و واریانس های برابر را در نظر بگیرید.

[math]{N_1(}{\mu}_{1}{,}{\sigma}^{2}{)}\qquad{N_2(}{\mu}_{2}{,}{\sigma}^{2}{)}[/math]

مقدار TVD به صورت ذیل محاسبه خواهد شد:

[math]{TVD}={[2\times\phi}{(\frac{\vert\mu_{1}-\mu_{2}\vert}{2\sigma}{)}}{]}{-1}[/math]

منظور از (.)φ مقدار به دست آمده از توزیع نرمال استاندارد می باشد.

مثال زیر را در نظر بگیرید. می خواهیم فاصله دو توزیع نرمال زیر را به دست آوریم:

[math]{N_1(5,4)}{,}\qquad{N_2(7,4)}[/math]

[math]{TVD}={[2\times\phi{(}}\frac{7-5}{2\times2}{)}{]}-{1}={2\times\phi{(0.5)}}{-1}[/math]

[math]\phi{(0.5)}=0.6915[/math]

مقدار (0.5)φ از جدول نرمال استاندارد برابر با 0.6915 به دست می آید. لذا مقدار TVD برابر است با:

[math]{TVD}={2\times0.6915}{-1}={0.383}[/math]

4- فاصله هلینگر

اگر دو تابع توزیع احتمال f و g داشته باشیم، مربع فاصله هلینگر عبارت خواهد شد از:

[math]{H}^{2}{(f,g)}=\frac{1}{2}\int{{(}\sqrt{f(x)}-\sqrt{g(x)}{)}}^{2}{dx}={1-}\int\sqrt{f(x)g(x)}{dx}[/math]

1-4- فاصله هلینگر برای دو تابع توزیع احتمال گسسته

در تابع توزیع احتمال گسسته P و Q را به ترتیب زیر در نظر بگیرید:

[math]{P}={{(}{p}_{1}{,}{p}_{2}{,}{…}{,}{p}_{k}{)}}[/math]

[math]{Q}={{(}{q}_{1}{,}{q}_{2}{,}{…}{,}{q}_{k}{)}}[/math]

در این صورت فاصله هلینگر بین این دو تابع توزیع برابر است با:

[math]{H(P,Q)}=\frac{1}{\sqrt{2}}\sqrt{{\sum_{i=1}^{K}}{(}{\sqrt{{p}_{i}}{-}\sqrt{{q}_{i}}{)}}^{2}}[/math]

2-4- فاصله هلینگر برای دو تابع توزیع نرمال

دو تابع توزیع نرمال P و Q را به ترتیب ذیل در نظر بگیرید.

[math]{P}\sim{N(}\mu_{1}{,}{\sigma_{1}}^{2}{)}[/math]

[math]{Q}\sim{N(}\mu_{2}{,}{\sigma_{2}}^{2}{)}[/math]

فاصله هلینگر برای این دو تابع توزیع احتمال برابر است با:

[math]{H}^{2}{(P,Q)}={1-}\sqrt\frac{{2\sigma}_{1}{\sigma}_{2}}{{\sigma_{1}}^{2}{+}{\sigma_{2}}^{2}}{e}^{{-}\frac{1}{4}\times\frac{(\mu_{1}{-}\mu_{2})^{2}}{{\sigma_{1}}^{2}{+}{\sigma_{2}}^{2}}}[/math]

3-4- فاصله هلینگر برای دو تابع توزیع نمایی

دو تابع توزیع نمایی P و Q را به ترتیب ذیل در نظر بگیرید.

[math]{P}\sim{Exp(}\alpha{)}[/math]

[math]{Q}\sim{Exp(}\beta{)}[/math]

[math]{H}^{2}{(P,Q)}={1-}\frac{2\sqrt{\alpha\beta}}{\alpha+\beta}[/math]

4-4- فاصله هلینگر برای دو تابع توزیع ویل بیول (Weilbull)

دو تابع توزیع ویل بیول P و Q را به ترتیب ذیل در نظر بگیرید.

[math]{P}\sim{W(}{k}{,}\alpha{)}[/math]

[math]{Q}\sim{W(}{k}{,}\beta{)}[/math]

[math]{H}^{2}{(P,Q)}={1-}\frac{{2(}{\alpha\beta)}^{\frac{k}{2}}}{{\alpha^{k}{+}\beta^{k}}}[/math]

5-4- فاصله هلینگر برای دو تابع توزیع پواسان

دو تابع توزیع پواسان P و Q را به ترتیب ذیل در نظر بگیرید.

[math]{P}\sim{Poisson(}\alpha{)}[/math]

[math]{Q}\sim{Poisson(}\beta{)}[/math]

[math]{H}^{2}{(P,Q)}={1-}{e}^{{-}\frac{1}{2}{(\sqrt\alpha}{-}{\sqrt\beta)}^{2}}[/math]

6-4- فاصله هلینگر برای دو تابع توزیع بتا

دو تابع توزیع بتای P و Q را به ترتیب ذیل در نظر بگیرید.

[math]{P}\sim{Beta({a}_{1}{,}{b}_{1})}[/math]

[math]{Q}\sim{Beta({a}_{2}{,}{b}_{2})}[/math]

[math]{H}^{2}{(P,Q)}={1-}\frac{{B(}\frac{{a_1}{+}{a_2}}{2}{,}\frac{{b_1}{+}{b_2}}{2}{)}}{\sqrt{B(a_1,b_1).B(a_2,b_2)}}[/math]

7-4- فاصله هلینگر برای دو تابع توزیع گاما

دو تابع توزیع گامای P و Q را به ترتیب ذیل در نظر بگیرید.

[math]{P}\sim{Gamma({a}_{1}{,}{b}_{1})}[/math]

[math]{Q}\sim{Gamma({a}_{2}{,}{b}_{2})}[/math]

[math]{H}^{2}{(P,Q)}={1-}\Gamma{(}\frac{a_1+a_2}{2}{)}{(}\frac{b_1+b_2}{2}{)}^{{-}\frac{(a_1+a_2)}{2}}\sqrt\frac{{{b_1}^{a_1}}{{b_2}^{a_2}}}{\Gamma{(a_1)}\Gamma{(a_2)}}[/math]